
(本小题满分14分)已知函数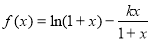 ,
,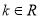 .
.
(1)讨论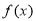 的单调区间;
的单调区间;
(2)当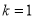 时,求
时,求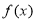 在
在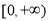 上的最小值,并证明
上的最小值,并证明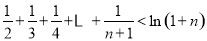 .
.
(1)当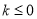 时,
时,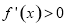 在
在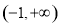 上恒成立,所以
上恒成立,所以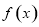 的单调递增区间是
的单调递增区间是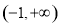 ,
,
无单调递减区间;当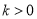 时,由
时,由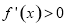 得
得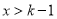 ,由
,由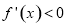 得
得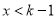 ,所以
,所以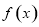 的单调递增区间是
的单调递增区间是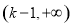 ,单调递减区间是
,单调递减区间是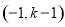 ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)函数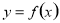 在某个区间内可导,则若
在某个区间内可导,则若 ,则
,则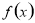 在这个区间内单调递增,若
在这个区间内单调递增,若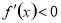 ,则
,则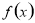 在这个区间内单调递减;(2)利用导数方法证明不等式
在这个区间内单调递减;(2)利用导数方法证明不等式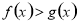 在区间
在区间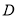 上恒成立的基本方法是构造函数
上恒成立的基本方法是构造函数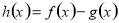 ,然后根据函数的单调性,或者函数的最值证明函数
,然后根据函数的单调性,或者函数的最值证明函数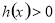 ,其中一个重要的技巧就是找到函数
,其中一个重要的技巧就是找到函数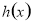 在什么地方可以等于零,这往往就是解决问题的一个突破口,观察式子的特点,找到特点证明不等式.
在什么地方可以等于零,这往往就是解决问题的一个突破口,观察式子的特点,找到特点证明不等式.
试题解析:【解析】
(1)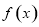 的定义域为
的定义域为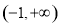 . (1分)
. (1分)
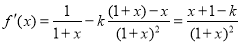 (3分)
(3分)
当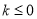 时,
时,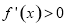 在
在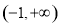 上恒成立,所以
上恒成立,所以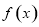 的单调递增区间是
的单调递增区间是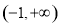 ,
,
无单调递减区间. (5分)
当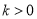 时,由
时,由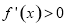 得
得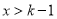 ,由
,由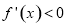 得
得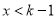 ,所以
,所以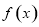 的单调递增区间是
的单调递增区间是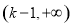 ,单调递减区间是
,单调递减区间是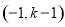 , (7分)
, (7分)
由(1)知,当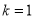 时,
时,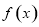 在
在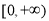 上单调递增,所以
上单调递增,所以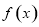 在
在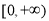 上的
上的
最小值为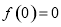 . (9分)
. (9分)
所以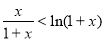 (
(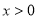 ) (10分)
) (10分)
所以 ,即
,即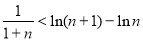 (
(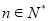 ). (12分)
). (12分)
所以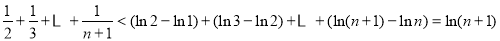 (14分)
(14分)
考点:1、利用导数求函数的单调区间;(2)证明不等式.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底理科数学试卷(解析版) 题型:选择题
设函数f(x)= sin2x+
sin2x+ cos2x,若将函数f(x)的图象向右平移
cos2x,若将函数f(x)的图象向右平移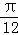 个单位,所得图象对应函数为g(x),则( )
个单位,所得图象对应函数为g(x),则( )
A.f(x)的图象关于直线x=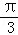 对称,g(x)图象关于原点对称
对称,g(x)图象关于原点对称
B.f(x)的图象关于点( ,0)对称,g(x)图象关于直线x=
,0)对称,g(x)图象关于直线x= 对称
对称
C.f(x)的图象关于直线x= 对称,g(x)图象关于原点对称
对称,g(x)图象关于原点对称
D.f(x)的图象关于点( ,0)对称,g(x)图象关于直线x=
,0)对称,g(x)图象关于直线x= 对称
对称
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省等六校高三第二次联考理科数学试卷(解析版) 题型:选择题
已知向量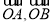 不共线,向量
不共线,向量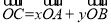 ,则下列命题正确的是
,则下列命题正确的是
A.若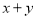 为定值,则
为定值,则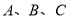 三点共线.
三点共线.
B.若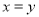 ,则点
,则点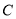 在
在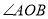 的平分线所在直线上.
的平分线所在直线上.
C.若点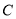 为
为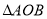 的重心,则
的重心,则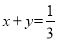 .
.
D.若点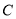 在
在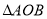 的内部(不含边界),则
的内部(不含边界),则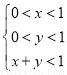 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市小学教学评估高毕业班第二次模拟文科数学试卷(解析版) 题型:选择题
已知等差数列{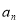 },
},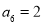 ,则此数列的前11项的和
,则此数列的前11项的和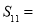
A.44 B.33 C.22 D.11
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市小学教学评估高毕业班第二次模拟理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知向量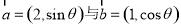 互相平行,其中
互相平行,其中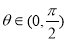 .
.
(1)求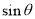 和
和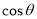 的值;
的值;
(2)若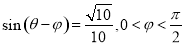 ,求
,求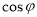 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省漳州市毕业班质量检查理科数学试卷(解析版) 题型:选择题
已知集合 (
( ,
, ),若数列
),若数列 是等差数列,记集合
是等差数列,记集合 的元素个数为
的元素个数为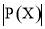 ,则
,则 关于
关于 的表达式为 .
的表达式为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省德阳市四校高三联合测试(3月)理科数学试卷(解析版) 题型:解答题
(本题满分12分)在数列{an}中,已知a =-20,a
=-20,a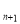 =a
=a +4(n∈
+4(n∈ ).
).
(1)求数列{an}的通项公式和前n项和An;
(2)若 (n∈
(n∈ ),求数列{bn}的前n项Sn.
),求数列{bn}的前n项Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com