练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．在数列{an}中，已知a1=2，a2=3，an+2=3an+1-2an（n≥1），写出此数列的前6项．

    分析 由递推公式a1=2，a2=3，an+2=3an+1-2an（n≥1）依次代入求解即可．

    解答 解：∵a1=2，a2=3，an+2=3an+1-2an（n≥1），
    ∴a3=3a2-2a1=9-4=5，
    ∴a4=3a3-2a2=9-4=15-6=9，
    ∴a5=3a4-2a3=9-4=27-10=17，
    ∴a6=3a5-2a4=9-4=51-18=33．

    点评 本题考查了数列的递推公式的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．物体以速度v（t）=3t2-2t+4做直线运动，它在第3s内的位移是（　　）
    A．12B．14C．16D．18

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知数列{an}中，a1=1，an+1=an+n．
    （1）写出数列{an}的前5项；
    （2）猜想数列{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．如图所示，三棱锥P-ABC的底面在平面α上，且AC⊥PC，平面PAC⊥平面PBC，点P，A，B是定点，则动点C运动形成的图形是（　　）
    A．一条线段B．一条直线
    C．一个圆D．一个圆，但要去掉两个点

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．设数列{an}的前n项和为Sn，已知a1=1，Sn-Sn-1=$\sqrt{{S}_{n}}$+$\sqrt{{S}_{n-1}}$（n≥2），求an．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．如图，双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的右顶点为A，左右焦点分别为F1，F2，点p是双曲线右支上一点，PF1交左支于点Q，交渐近线y=$\frac{b}{a}$x于点R，M是PQ的中点，若RF2⊥PF1，且AM⊥PF1，则双曲线的离心率是（　　）
    A．$\sqrt{2}$B．$\sqrt{3}$C．2D．$\sqrt{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知正数a，b满足ab=a+b+3．
    （1）求a+b的最小值；  
    （2）求ab的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．不等式-x2-2x+3≤0的解集为（-∞，-3]∪[1，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．如图，圆与两坐标轴分别切于A，B两点，圆上一动点P从A开始沿圆周按逆时针方向匀速旋转回到A点，则△OBP的面积随时间变化的图象符合（　　）
    A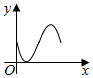．B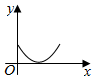．C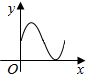．D．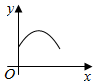

    查看答案和解析>>

    同步练习册答案