
分析 (1)由于正数a,b满足ab=a+b+3,可得a+b+3≤$(\frac{a+b}{2})^{2}$,化简解出即可得出.
(2)正数a,b满足ab=a+b+3,可得$ab≥2\sqrt{ab}+3$,化简解出即可得出.
解答 解:(1)∵正数a,b满足ab=a+b+3,
∴a+b+3≤$(\frac{a+b}{2})^{2}$,化为:(a+b)2-4(a+b)-12≥0,解得a+b≥6,∴a+b的最小值为6.
(2)∵正数a,b满足ab=a+b+3,∴$ab≥2\sqrt{ab}+3$,化为$(\sqrt{ab})^{2}$-2$\sqrt{ab}$-3≥0,解得$\sqrt{ab}$≥3,即ab≥9,
∴ab的取值范围是[9,+∞).
点评 本题考查了基本不等式的性质、一元二次不等式的解法,考查了推理能力与计算能力,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | 8-5$\sqrt{3}$ | B. | 6-5$\sqrt{3}$ | C. | 5$\sqrt{3}$-8 | D. | 5$\sqrt{3}$-6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
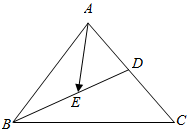 如图,△ABC中,D为AC中点,E为BD中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{b}$.
如图,△ABC中,D为AC中点,E为BD中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 零件数x(个) | 2 | 3 | 4 | 5 |
| 加工时间y(min) | 26 | 39 | 49 | 54 |
| A. | 63.6 min | B. | 65.5 min | C. | 67.7 min | D. | 72.0 min |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com