
【题目】如图,四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
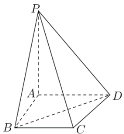
(1)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,计算出向量
,计算出向量![]() 、
、![]() ,然后利用空间向量法计算出异面直线
,然后利用空间向量法计算出异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)计算出平面![]() 的一个法向量
的一个法向量![]() ,平面
,平面![]() 的一个法向量
的一个法向量![]() ,然后利用空间向量法计算出二面角
,然后利用空间向量法计算出二面角![]() 的余弦值.
的余弦值.
(1)由题意可知,![]() 、
、![]() 、
、![]() 两两垂直,不妨以点
两两垂直,不妨以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,如下图所示:
,如下图所示:
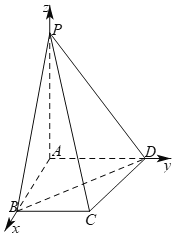
易得![]() ,则点
,则点![]() 、
、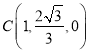 、
、![]() 、
、![]() .
.
![]() ,
,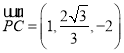 ,
,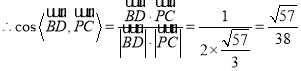 .
.
因此,异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ;
;
(2)易知点![]() 、
、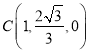 、
、![]() 、
、![]() .
.
易知平面![]() 的一个法向量为
的一个法向量为![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
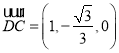 ,
,![]() ,
,
由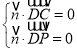 ,得
,得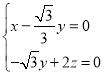 ,解得
,解得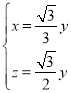 ,令
,令![]() ,则
,则![]() ,
,![]() ,
,
所以,平面![]() 的一个法向量为
的一个法向量为![]() ,
,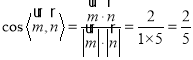 ,
,
由图象可知,二面角![]() 为锐角,它的余弦值为
为锐角,它的余弦值为![]() .
.


科目:高中数学 来源: 题型:
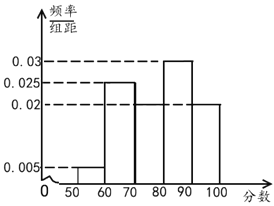
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
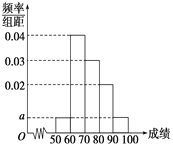
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
x∶y | 1∶1 | 2∶1 | 3∶4 | 4∶5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了纪念“一带一路”倡议提出五周年,某城市举办了一场知识竞赛,为了了解市民对“一带一路”知识的掌握情况,从回收的有效答卷中按青年组和老年组各随机抽取了40份答卷,发现成绩都在![]() 内,现将成绩按区间
内,现将成绩按区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,绘制成如下的频率分布直方图.
进行分组,绘制成如下的频率分布直方图.
青年组

中老年组
(1)利用直方图估计青年组的中位数和老年组的平均数;
(2)从青年组![]() ,
,![]() 的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自
的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自![]() 分数段的概率.
分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在![]() 上,且不恒为零的函数
上,且不恒为零的函数![]() 满足:对于任意实数
满足:对于任意实数![]() 和
和![]() ,总有
,总有![]() 恒成立,则称
恒成立,则称![]() 为“类余弦型”函数.
为“类余弦型”函数.
(1)已知![]() 为“类余弦型”函数,且
为“类余弦型”函数,且![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)证明:函数![]() 为偶函数;
为偶函数;
(3)若![]() 为“类余弦型”函数,且对于任意非零实数
为“类余弦型”函数,且对于任意非零实数![]() ,总有
,总有![]() ,设有理数
,设有理数![]() 、
、![]() 满足
满足![]() ,判断
,判断![]() 和
和![]() 大小关系,并证明你的结论.
大小关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知菱形![]() 的对角线
的对角线![]() 交于点
交于点![]() ,点
,点![]() 为线段
为线段![]() 的中点,
的中点,![]() ,
,![]() ,将三角形
,将三角形![]() 沿线段
沿线段![]() 折起到
折起到![]() 的位置,
的位置,![]() ,如图2所示.
,如图2所示.

(Ⅰ)证明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】身体素质拓展训练中,人从竖直墙壁的顶点A沿光滑杆自由下滑到倾斜的木板上(人可看作质点),若木板的倾斜角不同,人沿着三条不同路径AB、AC、AD滑到木板上的时间分别为t1、t2、t3,若已知AB、AC、AD与板的夹角分别为70o、90o和105o,则( )

A. t1>t2>t3 B. t1<t2<t3 C. t1=t2=t3 D. 不能确定t1、t2、t3之间的关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为两两不重合的平面,
为两两不重合的平面,![]() 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题:
(1)若![]() ,
,![]() ,则
,则![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,
,![]() 则
则![]() ;
;
(3)![]() ,
,![]() ,
,![]() ;
;
(4)若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
其中正确的命题是
A.(1)(3)B.(2)(3)C.(2)(4)D.(3)(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com