C
分析:由f(x)=x
3-2x
2-4x-7,知f′(x)=3x
2-4x-4,令f′(x)=3x
2-4x-4=0,得x
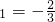
,x
2=2.列表讨论,知①错误,②正确;由a>2,x>2且x≠a,利用作差法知f(x)-f(a)-f′(a)(x-a)>0,故③正确;由f(x)=x
3-2x
2-4x-7,知函数f(x)不满足
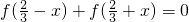
,故④不正确.
解答:∵f(x)=x
3-2x
2-4x-7,
∴f′(x)=3x
2-4x-4,
令f′(x)=3x
2-4x-4=0,得x
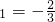
,x
2=2.
列表讨论
x (-∞,-

)-

(-

,2) 2(2,+∞) f′(x)- 0- 0+ f(x)↓ ↓ 极小值↑∴减区间为(-∞,2],增区间为[2,+∞),
当x=2时,函数有极小值f(2)=8-2×4-4×2-7=-15,
故①错误,②正确;
∵a>2,x>2且x≠a,
∴f(x)-f(a)-f′(a)(x-a)
=x
3-2x
2-4x-a
3+2a
2+4a-(3a
2-4a-4)(x-a)
=x
3+2a
3-2x
2-2a
2-3a
2x+4ax>0,
∴恒有f(x)>f(a)+f′(a)(x-a),
故③正确;
∵f(x)=x
3-2x
2-4x-7,
∴函数f(x)不满足
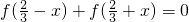
,
故④不正确,
故选C.
点评:本题考查函数的单调区间、极值的求法,考查不等式的应用,解题时要认真审题,仔细解答,注意等价转化思想和导数性质的灵活运用.

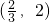 ;
;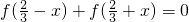
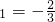 ,x2=2.列表讨论,知①错误,②正确;由a>2,x>2且x≠a,利用作差法知f(x)-f(a)-f′(a)(x-a)>0,故③正确;由f(x)=x3-2x2-4x-7,知函数f(x)不满足
,x2=2.列表讨论,知①错误,②正确;由a>2,x>2且x≠a,利用作差法知f(x)-f(a)-f′(a)(x-a)>0,故③正确;由f(x)=x3-2x2-4x-7,知函数f(x)不满足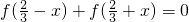 ,故④不正确.
,故④不正确.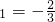 ,x2=2.
,x2=2. )-
)- (-
(- ,2) 2(2,+∞) f′(x)- 0- 0+ f(x)↓ ↓ 极小值↑∴减区间为(-∞,2],增区间为[2,+∞),
,2) 2(2,+∞) f′(x)- 0- 0+ f(x)↓ ↓ 极小值↑∴减区间为(-∞,2],增区间为[2,+∞),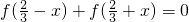 ,
,

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<