
ĄžĚâÄżĄżĐ˘¸ĐĐÇşÓĚě˝ÖšşÎďšăłĄÄłÓŞĎú˛żĂĹËćťúłé˛éÁË100ĂűĘĐĂńÔÚ2017ÄęšúÇ쳤źŮĆÚźäšşÎďšăłĄľÄĎűˇŃ˝đśîŁŹËůľĂĘýžÝČçąíŁŹŇŃÖŞĎűˇŃ˝đśî˛ťłŹšý3ǧԪÓ볏šý3ǧԪľÄČËĘýąČÇĄÎŞ3:2ŁŽ

Ł¨1ŁŠĘÔȡś¨![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ľÄÖľŁŹ˛˘˛šČŤĆľÂʡֲźÖąˇ˝ÍźŁ¨ČçÍźŁŠŁť
ľÄÖľŁŹ˛˘˛šČŤĆľÂʡֲźÖąˇ˝ÍźŁ¨ČçÍźŁŠŁť
Ł¨2ŁŠÓáֲăłéŃůľÄˇ˝ˇ¨´ÓĎűˇŃ˝đśîÔÚ![]() Ą˘
Ą˘![]() şÍ
şÍ![]() ľÄČý¸öČşĚĺÖĐłéČĄ7ČË˝řĐĐÎĘžíľ÷˛éŁŹÔň¸÷ĐĄ×éÓŚłéČĄź¸ČËŁżČô´ÓŐâ7ČËÖĐËćťúŃĄČĄ2ČËŁŹÔň´Ë2ČËŔ´×Ô͏ҝȺĚĺľÄ¸ĹÂĘĘÇśŕÉŮŁż
ľÄČý¸öČşĚĺÖĐłéČĄ7ČË˝řĐĐÎĘžíľ÷˛éŁŹÔň¸÷ĐĄ×éÓŚłéČĄź¸ČËŁżČô´ÓŐâ7ČËÖĐËćťúŃĄČĄ2ČËŁŹÔň´Ë2ČËŔ´×Ô͏ҝȺĚĺľÄ¸ĹÂĘĘÇśŕÉŮŁż
Ąž´đ°¸ĄżŁ¨1ŁŠźű˝âÎöŁ¨2ŁŠ2ŁŹ3ŁŹ2Łť ![]()
Ąž˝âÎöĄżĘÔĚâˇÖÎöŁşŁ¨1ŁŠ¸ůžÝŃůąžČÝÁżşÍĆľÂĘşÍÎŞ1żÉľĂšŘÓÚx,yľÄˇ˝łĚ×飏ÇóľĂ![]() ŁŹÓɴ˿ɾĂ
ŁŹÓɴ˿ɾĂ![]() ŁŹ
ŁŹ ![]() ŁŹ˝áşĎËůľĂĘýžÝżÉ˛šČŤĆľÂʡֲźÖąˇ˝ÍźĄŁŁ¨2ŁŠÓÉĆľÂʡֲźÖąˇ˝ÍźżÉľĂĎűˇŃ˝đśîÔÚ
ŁŹ˝áşĎËůľĂĘýžÝżÉ˛šČŤĆľÂʡֲźÖąˇ˝ÍźĄŁŁ¨2ŁŠÓÉĆľÂʡֲźÖąˇ˝ÍźżÉľĂĎűˇŃ˝đśîÔÚ![]() ŁŹ
ŁŹ ![]() ľÄČËĘýˇÖąđÎŞ2,3,2ČËŁŹÁОٿɾÝůąžĘÂźţ×ÜĘýš˛21¸öŁŹÉ襰2ČËŔ´×Ô͏ҝȺĚ她ΪĘÂźţ
ľÄČËĘýˇÖąđÎŞ2,3,2ČËŁŹÁОٿɾÝůąžĘÂźţ×ÜĘýš˛21¸öŁŹÉ襰2ČËŔ´×Ô͏ҝȺĚ她ΪĘÂźţ![]() ŁŹÔňM°üşŹ5¸öťůąžĘÂźţŁŹÓɚžä¸ĹĐ͸ĹÂĘšŤĘ˝żÉľĂ˝ášűĄŁ
ŁŹÔňM°üşŹ5¸öťůąžĘÂźţŁŹÓɚžä¸ĹĐ͸ĹÂĘšŤĘ˝żÉľĂ˝ášűĄŁ
ĘÔĚâ˝âÎöŁş
Ł¨1ŁŠ¸ůžÝĚâŇ⣏ÓĐ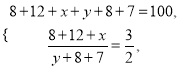
˝âľĂ![]()
Ąŕ![]() ŁŹ
ŁŹ ![]() ŁŽĄĄ
ŁŽĄĄ
˛šČŤĆľÂʡֲźÖąˇ˝ÍźČçÍźËůĘžŁş
Ł¨2ŁŠ¸ůžÝĚâŇ⣏ĎűˇŃ˝đśîÔÚ![]() ÄÚľÄČËĘýÎŞ
ÄÚľÄČËĘýÎŞ![]() Ł¨ČËŁŠŁŹźÇÎŞ
Ł¨ČËŁŠŁŹźÇÎŞ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ
ĎűˇŃ˝đśîÔÚ![]() ÄÚľÄČËĘýÎŞ
ÄÚľÄČËĘýÎŞ![]() Ł¨ČËŁŠŁŹźÇÎŞ1,2,3ŁŽĄĄ
Ł¨ČËŁŠŁŹźÇÎŞ1,2,3ŁŽĄĄ
ĎűˇŃ˝đśîÔÚ![]() ÄÚľÄČËĘýÎŞ
ÄÚľÄČËĘýÎŞ![]() Ł¨ČËŁŠŁŹźÇÎŞ
Ł¨ČËŁŠŁŹźÇÎŞ![]() ŁŹ
ŁŹ ![]() ŁŽ
ŁŽ
Ôň´ÓŐâ7ČËÖĐËćťúŃĄČĄ2ČËľÄËůÓоĝůąžĘÂźţÎŞŁş ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹš˛21ÖÖŁŹ
ŁŹš˛21ÖÖŁŹ
É襰2ČËŔ´×Ô͏ҝȺĚ她ΪĘÂźţ![]() ŁŹÔňĘÂźţ
ŁŹÔňĘÂźţ![]() °üşŹľÄťůąžĘÂźţÓĐ
°üşŹľÄťůąžĘÂźţÓĐ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() ŁŹš˛5ÖÖŁŹ
ŁŹš˛5ÖÖŁŹ
Óɚžä¸ĹĐ͸ĹÂĘšŤĘ˝ľĂ![]() ŁŽ
ŁŽ
ËůŇÔ´Ë2ČËŔ´×Ô͏ҝȺĚĺľÄ¸ĹÂĘĘÇ![]() ĄŁ
ĄŁ



| Äęźś | ¸ßÖĐżÎłĚ | Äęźś | łőÖĐżÎłĚ |
| ¸ßŇť | ¸ßŇťĂâˇŃżÎłĚÍĆźöŁĄ | łőŇť | łőŇťĂâˇŃżÎłĚÍĆźöŁĄ |
| ¸ßśţ | ¸ßśţĂâˇŃżÎłĚÍĆźöŁĄ | łőśţ | łőśţĂâˇŃżÎłĚÍĆźöŁĄ |
| ¸ßČý | ¸ßČýĂâˇŃżÎłĚÍĆźöŁĄ | łőČý | łőČýĂâˇŃżÎłĚÍĆźöŁĄ |
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
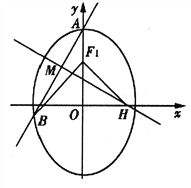
ĄžĚâÄżĄżŇŃÖŞÍÖÔ˛![]() ľÄÉĎĄ˘Ď½šľăˇÖąđÎŞ
ľÄÉĎĄ˘Ď½šľăˇÖąđÎŞ![]() ŁŹÉĎ˝šľă
ŁŹÉĎ˝šľă![]() ľ˝ÖąĎß 4x+3y+12=0ľÄžŕŔëÎŞ3ŁŹÍÖÔ˛CľÄŔëĐÄÂĘe=
ľ˝ÖąĎß 4x+3y+12=0ľÄžŕŔëÎŞ3ŁŹÍÖÔ˛CľÄŔëĐÄÂĘe=![]() ŁŽ
ŁŽ
(I)ÇóÍÖÔ˛CľÄąęןˇ˝łĚŁť
(II)ÉčšýÍÖÔ˛CľÄÉĎśĽľăAľÄÖąĎß![]() ÓëÍÖÔ˛˝ťÓÚľăB(B˛ťÔÚyÖáÉĎ)ŁŹ´šÖąÓÚ
ÓëÍÖÔ˛˝ťÓÚľăB(B˛ťÔÚyÖáÉĎ)ŁŹ´šÖąÓÚ![]() ľÄÖąĎßÓë
ľÄÖąĎßÓë![]() ˝ťÓÚľăMŁŹÓë
˝ťÓÚľăMŁŹÓë![]() ÖὝÓÚľăHŁŹČô
ÖὝÓÚľăHŁŹČô![]() =0ŁŹÇŇ
=0ŁŹÇŇ![]() ŁŹÇóÖąĎß
ŁŹÇóÖąĎß![]() ľÄˇ˝łĚŁŽ
ľÄˇ˝łĚŁŽ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżŇŃÖŞÍÖÔ˛![]() Łş
Łş ![]() ŁŹÉčÖąĎß
ŁŹÉčÖąĎß![]() ÓëÍÖÔ˛
ÓëÍÖÔ˛![]() ˝ťÓÚ˛ťÍŹÁ˝ľă
˝ťÓÚ˛ťÍŹÁ˝ľă![]() ŁŹÇŇ
ŁŹÇŇ![]() ŁŽČôľă
ŁŽČôľă![]() Âú×ă
Âú×ă![]() ŁŹÔň
ŁŹÔň![]() =______________.
=______________.
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżĐ˘¸ĐĘĐź°ÖÜąßľŘÇřľÄĘĐĂńÓÎÍćÓÖĚíĐÂČĽ´ŚŔ˛ŁĄĐ˘¸ĐÎőˇďËŽĎçÂĂÓΜȟŮÇřÓÚ2017Äę10ÔÂ1ČŐŐýĘ˝śÔÍ⿪ˇĹŁŽžÝÍłźĆŁŹ´Ó2017Äę10ÔÂ1ČŐľ˝10ÔÂ7ČղΚŰТ¸ĐĘĐÎőˇďËŽĎçÂĂÓΜȟŮÇřľÄČËĘýČçąíËůĘžŁş
ČŐĆÚ | 1ČŐ | 2ČŐ | 3ČŐ | 4ČŐ | 5ČŐ | 6ČŐ | 7ČŐ |
ČËĘýŁ¨ÍňŁŠ | 11 | 13 | 8 | 9 | 7 | 8 | 10 |
Ł¨1ŁŠ°ŃŐâ7ĚěľÄ˛ÎšŰČËĘýż´łÉŇť¸ö×ÜĚ壏Çó¸Ă×ÜĚĺľÄÖÚĘýşÍĆ˝žůĘýŁ¨žŤČˇľ˝0.1ŁŠŁť
Ł¨2ŁŠÓĂźňľĽËćťúłéŃůˇ˝ˇ¨´Ó10ÔÂ1ČŐľ˝10ÔÂ4ČŐÖĐłéČĄ2Ě죏ËüĂǾIJΚŰČËĘý×éłÉŇť¸öŃůąžŁŹÇó¸ĂŃůąžĆ˝žůĘýÓë×ÜĚĺĆ˝žůĘýÖŽ˛îľÄžřśÔÖľ˛ťłŹšý1ÍňľÄ¸ĹÂĘŁŽ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżŇŃÖŞÍÖÔ˛![]() ľÄŔëĐÄÂĘĘÇ
ľÄŔëĐÄÂĘĘÇ![]() ŁŹÇŇšýľă
ŁŹÇŇšýľă![]() .ÖąĎß
.ÖąĎß![]() ÓëÍÖÔ˛
ÓëÍÖÔ˛![]() ĎཝÓÚ
ĎཝÓÚ![]() Á˝ľă.
Á˝ľă.
Ł¨˘ńŁŠÇóÍÖÔ˛![]() ľÄˇ˝łĚŁť
ľÄˇ˝łĚŁť
Ł¨˘ňŁŠÇó![]() ľÄĂćťýľÄ×î´óÖľŁť
ľÄĂćťýľÄ×î´óÖľŁť
Ł¨˘óŁŠÉčÖąĎß![]() ŁŹ
ŁŹ ![]() ˇÖąđÓë
ˇÖąđÓë![]() ÖὝÓÚľă
ÖὝÓÚľă![]() ŁŹ
ŁŹ ![]() .ĹĐśĎ
.ĹĐśĎ![]() ŁŹ
ŁŹ ![]() ´óĐĄšŘĎľŁŹ˛˘źÓŇÔÖ¤Ă÷.
´óĐĄšŘĎľŁŹ˛˘źÓŇÔÖ¤Ă÷.
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżŇŃÖŞÍÖÔ˛![]() ľÄÓŇ˝šľă
ľÄÓŇ˝šľă![]() ŁŹÍÖÔ˛
ŁŹÍÖÔ˛![]() ľÄ×óŁŹÓŇśĽľăˇÖąđÎŞ
ľÄ×óŁŹÓŇśĽľăˇÖąđÎŞ![]() ŁŽšýľă
ŁŽšýľă![]() ľÄÖąĎß
ľÄÖąĎß![]() ÓëÍÖÔ˛˝ťÓÚ
ÓëÍÖÔ˛˝ťÓÚ![]() Á˝ľăŁŹÇŇ
Á˝ľăŁŹÇŇ![]() ľÄĂćťýĘÇ
ľÄĂćťýĘÇ![]() ľÄĂćťýľÄ3ąśŁŽ
ľÄĂćťýľÄ3ąśŁŽ
Ł¨˘ńŁŠÇóÍÖÔ˛![]() ľÄˇ˝łĚŁť
ľÄˇ˝łĚŁť
Ł¨˘ňŁŠČô![]() Óë
Óë![]() Öá´šÖąŁŹ
Öá´šÖąŁŹ![]() ĘÇÍÖÔ˛
ĘÇÍÖÔ˛![]() ÉĎÎťÓÚÖąĎß
ÉĎÎťÓÚÖąĎß![]() Á˝˛ŕľÄśŻľăŁŹÇŇÂú×ă
Á˝˛ŕľÄśŻľăŁŹÇŇÂú×ă![]() ŁŹĘÔÎĘÖąĎß
ŁŹĘÔÎĘÖąĎß![]() ľÄĐąÂĘĘǡńÎŞś¨ÖľŁŹÇëËľĂ÷ŔíÓÉŁŽ
ľÄĐąÂĘĘǡńÎŞś¨ÖľŁŹÇëËľĂ÷ŔíÓÉŁŽ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżĹМϺŻĘýfŁ¨xŁŠ= ![]() ÔÚŁ¨Š1ŁŹ+ĄŢŁŠÉϾľĽľ÷ĐÔŁŹ˛˘Ö¤Ă÷ŁŽ
ÔÚŁ¨Š1ŁŹ+ĄŢŁŠÉϾľĽľ÷ĐÔŁŹ˛˘Ö¤Ă÷ŁŽ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżÄłšŤËž2016ÄęÇ°Čý¸öÔÂľÄŔűČ󣨾ĽÎťŁş°ŮÍňÔŞŁŠČçĎÂŁş
ÔÂˇÝ | 1 | 2 | 3 |
ŔűČó | 2 | 3.9 | 5.5 |
Ł¨1ŁŠÇóŔűČó![]() šŘÓÚÔ¡Ý
šŘÓÚÔ¡Ý![]() ľÄĎßĐԝؚ顽łĚŁť
ľÄĎßĐԝؚ顽łĚŁť
Ł¨2ŁŠĘÔÓĂŁ¨1ŁŠÖĐÇóľĂľÄťŘšéˇ˝łĚÔ¤˛â4ÔÂşÍ5ÔÂľÄŔűČóŁť
Ł¨3ŁŠĘÔÓĂŁ¨1ŁŠÖĐÇóľĂľÄťŘšéˇ˝łĚÔ¤˛â¸ĂšŤËž2016Äę´Óź¸Ô¡ݿŞĘźŔűČ󳏚ý1000ÍňŁż
ĎŕšŘšŤĘ˝Łş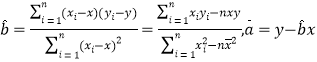 .
.
˛éż´´đ°¸şÍ˝âÎö>>
šúźĘѧУÓĹŃĄ - ÁˇĎ°˛áÁĐąí - ĘÔĚâÁĐąí
şţąąĘĄťĽÁŞÍřÎĽˇ¨şÍ˛ťÁźĐĹϢžŮą¨Ć˝Ě¨ | ÍřÉĎÓĐşŚĐĹϢžŮą¨×¨Çř | ľçĐĹՊƞٹ¨×¨Çř | ÉćŔúʡĐéÎŢÖ÷ŇĺÓĐşŚĐĹϢžŮą¨×¨Çř | ÉćĆóÇÖȨžŮą¨×¨Çř
ÎĽˇ¨şÍ˛ťÁźĐĹϢžŮą¨ľçť°Łş027-86699610 žŮą¨ÓĘĎ䣺58377363@163.com