
【题目】已知椭圆![]() :
: ![]() ,设直线
,设直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() ,且
,且![]() .若点
.若点![]() 满足
满足![]() ,则
,则![]() =______________.
=______________.
【答案】![]() 或
或![]()
【解析】由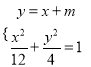 ,得
,得![]() ①
①
∵直线l与椭圆C交于不同两点![]() ,
,
∴![]() 得
得![]() <16.
<16.
设![]() 则
则![]() ,
,![]() 是方程①的两根,
是方程①的两根,
则![]() .
.
∴![]() .
.
又由![]() ,得
,得![]() ,解之m=±2.
,解之m=±2.
据题意知,点P为线段AB的中垂线与直线y=2的交点。
设AB的中点为![]() ,则
,则![]() ,
,
当m=2时, ![]() .
.
∴此时,线段AB的中垂线方程为![]() ,即y=x1.
,即y=x1.
令y=2,得![]() =3.
=3.
当m=2时,E(![]() ,
,![]() ).
).
∴此时,线段AB的中垂线方程为![]() ,即y=x+1.
,即y=x+1.
令y=2,得![]() =1.
=1.
综上所述, ![]() 的值为3或1.
的值为3或1.
点睛: 本题主要考查直线与圆锥曲线位置关系,所使用方法为韦达定理法:因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用韦达定理直接解决,但应注意不要忽视判别式的作用.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】已知A={x|(2x)2﹣62x+8≤0},函数f(x)=log2x(x∈A).
(1)求函数f(x)的定义域;
(2)若函数h(x)=[f(x)]2﹣log2(2x),求函数h(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|﹣1≤x≤10},集合B={x|2x﹣6≥0}.
求R(A∪B);
已知C={x|a<x<a+1},且CA,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知椭圆![]() 的焦距为
的焦距为 ![]() ,直线
,直线![]() 被椭圆
被椭圆 ![]() 截得的弦长为
截得的弦长为![]() .
.

(1)求椭圆 ![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆 ![]() 上的动点,过原点
上的动点,过原点![]() 引两条射线
引两条射线![]() 与圆
与圆![]() 分别相切,且
分别相切,且![]() 的斜率
的斜率![]() 存在. ①试问
存在. ①试问 ![]() 是否为定值?若是,求出该定值,若不是,说明理由;
是否为定值?若是,求出该定值,若不是,说明理由;
②若射线![]() 与椭圆
与椭圆 ![]() 分别交于点
分别交于点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,点 ![]() 的极坐标是
的极坐标是![]() ,曲线
,曲线 ![]() 的极坐标方程为
的极坐标方程为![]() .以极点为坐标原点,极轴为
.以极点为坐标原点,极轴为 ![]() 轴的正半轴建立平面直角坐标系,斜率为
轴的正半轴建立平面直角坐标系,斜率为 ![]() 的直线
的直线 ![]() 经过点
经过点![]() .
.
(1)写出直线 ![]() 的参数方程和曲线
的参数方程和曲线 ![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线 ![]() 和曲线
和曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孝感星河天街购物广场某营销部门随机抽查了100名市民在2017年国庆长假期间购物广场的消费金额,所得数据如表,已知消费金额不超过3千元与超过3千元的人数比恰为3:2.

(1)试确定![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值,并补全频率分布直方图(如图);
的值,并补全频率分布直方图(如图);
(2)用分层抽样的方法从消费金额在![]() 、
、![]() 和
和![]() 的三个群体中抽取7人进行问卷调查,则各小组应抽取几人?若从这7人中随机选取2人,则此2人来自同一群体的概率是多少?
的三个群体中抽取7人进行问卷调查,则各小组应抽取几人?若从这7人中随机选取2人,则此2人来自同一群体的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com