
【题目】设函数y=x3与y=( ![]() )x的图象的交点为(x0 , y0),若x0所在的区间是(k,k+1)(k∈Z),则k= .
)x的图象的交点为(x0 , y0),若x0所在的区间是(k,k+1)(k∈Z),则k= .
【答案】0
【解析】解:由于函数y=x3与y=( ![]() )x的图象的交点为(x0 , y0),
)x的图象的交点为(x0 , y0),
∵( ![]() )x>0,∴x3>0,∴x0>0.
)x>0,∴x3>0,∴x0>0.
函数f(x)=x3 ﹣( ![]() )x的零点为x0 .
)x的零点为x0 .
再根据f(1)= ![]() >0,f(0)=﹣1<0,f(1)f(0)<0,故f(x)的零点为x0∈(0,1),
>0,f(0)=﹣1<0,f(1)f(0)<0,故f(x)的零点为x0∈(0,1),
可得k=0.
所以答案是:0.
【考点精析】关于本题考查的函数的零点与方程根的关系,需要了解二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某企业生产一种机器的固定成本为0.5万元,但每生产1百台时,又需可变成本(即另增加投入)0.25万元.市场对此商品的年需求量为5百台,销售的收入(单位:万元)函数为:R(x)=5x﹣ ![]() x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
(1)将利润表示为产量的函数;
(2)年产量是多少时,企业所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1,F2分别是椭圆E: ![]() (a>b>0)的左、右焦点,过点F1的直线交椭圆E于A,B两点,|AF1|=3|BF1|,若cos∠AF2B=
(a>b>0)的左、右焦点,过点F1的直线交椭圆E于A,B两点,|AF1|=3|BF1|,若cos∠AF2B=![]() ,则椭圆E的离心率为( )
,则椭圆E的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,上焦点
,上焦点![]() 到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=
到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=![]() .
.
(I)求椭圆C的标准方程;
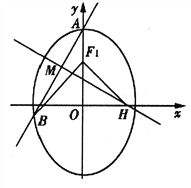
(II)设过椭圆C的上顶点A的直线![]() 与椭圆交于点B(B不在y轴上),垂直于
与椭圆交于点B(B不在y轴上),垂直于![]() 的直线与
的直线与![]() 交于点M,与
交于点M,与![]() 轴交于点H,若
轴交于点H,若![]() =0,且
=0,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
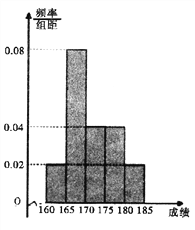
【题目】近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如下图所示:
(I)在第3、4、5组中用分层抽样抽取5名选手,求第3、4、5组每组各抽取多少名选手;
(II)在(I)的前提下,在5名选手中随机抽取2名选手,求第4组至少有一名选手被抽取的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲厂根据以往的生产销售经验得到下面有关生产销售的关系:厂里的固定成本为2.8万元,每生产1百台的生产成本为1万元,每生产产品x(百台),其总成本为G(x)(万元)(总成本=固定成本+生产成本).如果销售收入R(x)= ![]() ,且该产品产销平衡(即生产的产品都能卖掉),请完成下列问题:
,且该产品产销平衡(即生产的产品都能卖掉),请完成下列问题:
(1)写出利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)甲厂生产多少台新产品时,可使盈利最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 的左,右顶点分别为
的左,右顶点分别为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() 的面积是
的面积是![]() 的面积的3倍.
的面积的3倍.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 与
与![]() 轴垂直,
轴垂直,![]() 是椭圆
是椭圆![]() 上位于直线
上位于直线![]() 两侧的动点,且满足
两侧的动点,且满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com