
 已知椭圆C:$\frac{x^2}{3}+{y^2}$=1,过点M(2,0)任作一条直线与C交于不同的两点A、B.
已知椭圆C:$\frac{x^2}{3}+{y^2}$=1,过点M(2,0)任作一条直线与C交于不同的两点A、B.分析 (1)联立方程组,利用韦达定理,结合三角形的面积公式,即可求△OAB的面积的最大值;
(2)由(1)知:$\frac{1}{y_1}+\frac{1}{y_2}=-4t$,再求出$\frac{1}{y_3}$+$\frac{1}{y_4}$,即可证明结论.
解答 (1)解:联立方程组$\left.{\begin{array}{l}{x=ty+2}\\{{x^2}+3{y^2}=3}\end{array}}\right\}⇒(3+{t^2}){y^2}+4ty+1=0⇒\left\{{\begin{array}{l}{{y_1}+{y_2}=-\frac{4t}{{3+{t^2}}}}\\{{y_1}{y_2}=\frac{1}{{3+{t^2}}}}\end{array}}\right.$
由△>0⇒t2>1
所以$|{{y_1}-{y_2}}|=\sqrt{\frac{{12({t^2}-1)}}{{{{({t^2}+3)}^2}}}}=\sqrt{\frac{12}{{{t^2}-1+\frac{16}{{{t^2}-1}}+8}}}≤\frac{{\sqrt{3}}}{2}$
所以${S_{△AOB}}=\frac{1}{2}|{OM}||{{y_1}-{y_2}}|≤\frac{{\sqrt{3}}}{2}$.----------------(6分)
(2)证明:由(1)知:$\frac{1}{y_1}+\frac{1}{y_2}=-4t$------------------(8分)
NA:$y=\frac{y_1}{{{x_1}+\sqrt{3}}}(x+\sqrt{3})⇒{y_3}=(\frac{3}{2}+\sqrt{3})\frac{y_1}{{{x_1}+\sqrt{3}}}$,同理:${y_4}=(\frac{3}{2}+\sqrt{3})\frac{y_2}{{{x_2}+\sqrt{3}}}$$\frac{1}{y_3}+\frac{1}{y_4}=\frac{1}{{\frac{3}{2}+\sqrt{3}}}(\frac{{{x_1}+\sqrt{3}}}{y_1}+\frac{{{x_2}+\sqrt{3}}}{y_2})=-4t$.
故$\frac{1}{y_1}+\frac{1}{y_2}=\frac{1}{y_3}+\frac{1}{y_4}$----------------(12分)
点评 本题考查直线与椭圆的位置关系,考查三角形面积的计算,考查韦达定理的运用,正确运用韦达定理是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x0∈(-4,-3) | B. | x0∈(-3,-2) | C. | x0∈(-2,-1) | D. | x0∈(-1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
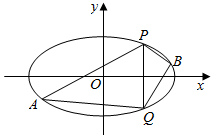 已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,它的一个顶点恰好是抛物线x2=4$\sqrt{2}$y的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,它的一个顶点恰好是抛物线x2=4$\sqrt{2}$y的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com