
科目:高中数学 来源: 题型:
已知各项均为正数的 等比数列{
等比数列{ }的首项为a1=2,且4a1是2a2
}的首项为a1=2,且4a1是2a2 ,a3等差中项.
,a3等差中项.
(1)求数列{ }的通项公
}的通项公 式
式 ;
;
(2)若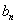 =
=
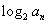 ,
,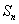 =b1+b2+…+
=b1+b2+…+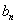 ,求
,求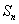 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆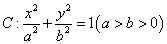 过点
过点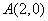 ,离心率为
,离心率为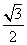 .
.
(Ⅰ)求椭圆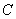 的方程;
的方程;
(Ⅱ)过点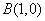 且斜率为
且斜率为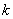 (
(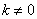 )的直线
)的直线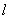 与椭圆
与椭圆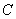 相交于
相交于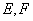 两点,直线
两点,直线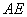 ,
,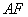 分别交直线
分别交直线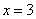 于
于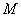 ,
, 两点,线段
两点,线段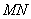 的中点为
的中点为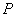 .记直线
.记直线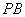 的斜率为
的斜率为 ,求证:
,求证: 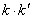 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
国家环境标准制定的空气质量指数与空气质量等级对应关系如下表:
| 空气质量指数 | 0-50 | 51-100 | 101-150 | 151-200 | 201-300 | 300以上 |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
由全国重点城市环境监测网获得2月份某五天甲城市和乙城市的空气质量指数数据用茎叶图表示如下:
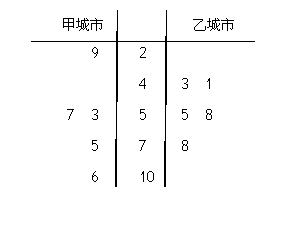
(Ⅰ)试根据上面的统计数据,判断甲、乙两个城市的空气质量指数的方差的大小关系(只需写出结果);
(Ⅱ)试根据上面的统计数据,估计甲城市某一天空气质量等级为2级良的概率;
(Ⅲ)分别从甲城市和乙城市的统计数据中任取一个,试求这两个城市空气质量等级相同的概率.
(注: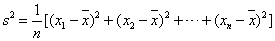 ,其中
,其中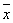 为数据
为数据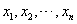 的平均数.)
的平均数.)
查看答案和解析>>
科目:高中数学 来源: 题型:
设满足以下两个条件的有穷数列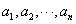 为n(n=2,3,4,…,)阶“期待数列”:
为n(n=2,3,4,…,)阶“期待数列”:
① 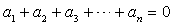 ;
;
② 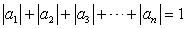 .
.
(Ⅰ)分别写出一个单调递增的3阶和4阶“期待数列”;
(Ⅱ)若某2013阶“期待数列”是等差数列,求该数列的通项公式;
(Ⅲ)记n阶“期待数列”的前k项和为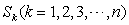 ,试证:
,试证: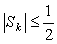 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com