
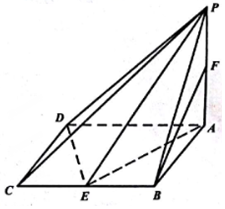
 在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PA=$\sqrt{3}$,PA⊥面ABCD,E、F分别为BC、PA的中点.
在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PA=$\sqrt{3}$,PA⊥面ABCD,E、F分别为BC、PA的中点.分析 (1)取PD中的G,连结GF、GE,得到四边形BFGE是平行四边形,即可得到BF∥平面PDE.
(Ⅱ)作DH⊥AE与E,作HI⊥PE于I,连结DI,可得∠DIH即为二面角D-PE-A的平面角,
在直角△DIH中,求解sin∠DIH即可
(Ⅲ)设点C到平面PDE的距离为h,
由VP-CDE=VC-PDE,求得h,即为点C到平面PDE的距离
解答 解:(1)如图所示,取PD中的G,连结GF、GE,
∵E、F分别为BC、PA的中点.∴FG∥BE,FG=BE.
所以四边形BFGE是平行四边形,
∴BF∥平面PDE.
(Ⅱ)作DH⊥AE与E,作HI⊥PE于I,连结DI,可得DH⊥面PAB,
∴DH⊥PE,又因为PE⊥HI,HI∩DH=H,∴PE⊥面DIH,∴PE⊥DI
∴∠DIH即为二面角D-PE-A的平面角,
在直角△DIH中,sin∠DIH=$\frac{DH}{DI}=\frac{2\sqrt{10}}{7}$,
∴二面角D-PE-A的正弦值为$\frac{2\sqrt{10}}{7}$.
(Ⅲ)设点C到平面PDE的距离为h,
∵VP-CDE=VC-PDE,∴$\frac{1}{3}{s}_{△CDE}×PA=\frac{1}{3}{s}_{△PDE}×h$,
$\frac{\sqrt{3}}{2}×\sqrt{3}=\frac{1}{2}×\sqrt{3}×\sqrt{7}×h$,解得h=$\frac{\sqrt{21}}{7}$,
∴点C到平面PDE的距离为$\frac{\sqrt{21}}{7}$.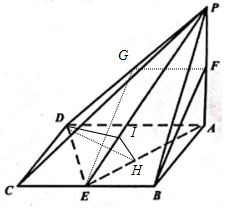
点评 本小题主要考查直线平行与平面的判定,以及几何法求二面角,等体积法求点面距离,考查空间想象能力、运算能力和推理论证能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设定义域为R的函数f(x)=$\left\{\begin{array}{l}{x+1,(x≤0)}\\{{x}^{2}-2x+1,(x>0)}\end{array}\right.$.
设定义域为R的函数f(x)=$\left\{\begin{array}{l}{x+1,(x≤0)}\\{{x}^{2}-2x+1,(x>0)}\end{array}\right.$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 资源 产品 | 资金(万元) | 场地(平方米) |
| A | 2 | 100 |
| B | 3 | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com