练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知△ABC的内角A、B、C所对应边分别为a，b，c，若3a2+2ab+3b2－3c2=0，则sinC的值是（    ）

    A．

    B．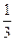

    C．

    D．

     

    C

    【解析】∵3a2+2ab+3b2－3c2=0，∴a2+b2－c2=ab

    由余弦定理知cosC==－

    又sin2C+cos2C=1

    ∴sinC=

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014高考名师推荐数学理科利用导数求最值和极值（解析版） 题型：选择题

    已知函数在区间[－1，2]上是减函数，那么b+c(    )

    A．有最大值

    B．有最大值－

    C．有最小值

    D．有最小值－

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科函数与方程（解析版） 题型：选择题

    设函数满足，，且当时，．又函数，则函数在上的零点个数为（ ）

    A．5 B．6 C．7 D．8

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科全称量词与存在性量词（解析版） 题型：选择题

    已知命题p1：函数y＝2x－2－x在R上为增函数，p2：函数y＝2x＋2－x在R上为减函数，则在命题q1：p1∨p2，q2：p1∧p2，q3：(?p1)∨p2和q4：p1∧(?p2)中，真命题是

    A. q1，q3

    B. q2，q3

    C. q1，q4

    D. q2，q4

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科余弦定理（解析版） 题型：解答题

    △ABC在内角A、B、C的对边分别为a，b，c，已知a=bcosC+csinB．

    （1）求B；

    （2）若b=2，求△ABC面积的最大值。

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科二项式定理与性质（解析版） 题型：填空题

    若＝xn＋…＋ax3＋bx2＋…＋1（n∈N*），且a∶b＝3∶1，那么n=_____．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科二项式定理与性质（解析版） 题型：选择题

    展开式中的常数项???( )

    A．80 B．－80 C．40 D．－40

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科不等式选讲（解析版） 题型：解答题

    已知函数f(x)=|x－a|,其中a>1.

    (1)当a=2时,求不等式f(x)≥4－|x－4|的解集;

    (2)已知关于x的不等式|f(2x+a)－2f(x)|≤2的解集为{x|1≤x≤2},求a的值.

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科预测题（解析版） 题型：填空题

    如图，AB是⊙O的一条切线，切点为B，ADE、CFD都是⊙O的割线，AC=AB.

    （1）证明：AC2=AD·AE

    （2）证明：FG∥AC

     

     

    查看答案和解析>>

    同步练习册答案