
| A�� | �٢� | B�� | �ڢ� | C�� | �٢� | D�� | �� |
���� �ٸ���ƽ�������Ļ��������������̽�����⼴�ɣ�
�ڸ������Ǻ����ı��ǹ�ʽ������⣮
�۸������Ǻ����Գ��Խ�����⣮
�ܸ��ݺ�����ż�Ժ͵�����֮��Ĺ�ϵ��������Ǻ������յ���ʽ������⼴�ɣ�
��� �⣺����֪$\overrightarrow a$=��-1��-2����$\overrightarrow b$=��1��1����$\overrightarrow c$=��3��-2������$\overrightarrow c$=p$\overrightarrow a$+q$\overrightarrow b$��
��$\left\{\begin{array}{l}{-p+q=3}\\{-2p+q=-2}\end{array}\right.$��p=5��q=8���ʢٴ���
�ڡ�sin��cos��=$\frac{1}{2}$sin����[$-\frac{1}{2}$��$\frac{1}{2}$]�������ʵ������ʹsin��cos��=1���ʢ���ȷ��
�۵�x=$\frac{��}{8}$ʱ��y=sin��2x+$\frac{5}{4}��$��=sin��2��$\frac{��}{8}$+$\frac{5}{4}��$��=sin$\frac{3��}{2}$=-1��0��
�ࣨ$\frac{��}{8}$��0�����Ǻ���y=sin��2x+$\frac{5}{4}��$����һ���Գ������ģ��ʢ۴���
������ABC�����������
��A+C��$\frac{��}{2}$����A��$\frac{��}{2}$-C��
��sinA��sin��$\frac{��}{2}$-C��=cosC��
�ߺ���f��x���ڣ�0��1����Ϊ������������ǡ�ABC�У���f��sinA����f��cosC�����ʢ���ȷ��
��ѡ��B
���� ������Ҫ�������������жϣ��漰ƽ�������Ļ������������Ǻ�������ż�Ժ͵�����֮��Ĺ�ϵ���ۺ��Խ�ǿ���ѶȲ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���������ι��ţ���ˮ����ʱ��������ˮ��2m��ˮ���4m�����ˮλ�½�$\frac{5}{2}$m��ˮ�����5m����ˮ�����Ϊ��������
��ͼ���������ι��ţ���ˮ����ʱ��������ˮ��2m��ˮ���4m�����ˮλ�½�$\frac{5}{2}$m��ˮ�����5m����ˮ�����Ϊ��������| A�� | 1m | B�� | 6m | C�� | $2\sqrt{5}$m | D�� | 4m |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{5}+1}}{2}$ | B�� | $\sqrt{5}-1$ | C�� | $\sqrt{2}$ | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
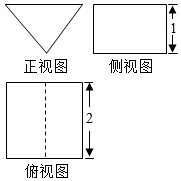 �������������У���������ֱ�������ε�ֱ��������֮Ϊ��ǵ�¡�����֪ij��ǵ�¡�������ͼ��ͼ��ʾ������ͼ������ƽ�־��ε��������á�ǵ�¡��IJ����Ϊ��������
�������������У���������ֱ�������ε�ֱ��������֮Ϊ��ǵ�¡�����֪ij��ǵ�¡�������ͼ��ͼ��ʾ������ͼ������ƽ�־��ε��������á�ǵ�¡��IJ����Ϊ��������| A�� | 2 | B�� | 4+2$\sqrt{2}$ | C�� | 4+4$\sqrt{2}$ | D�� | 6+4$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ŷ����ʦ���ø�ʱ��ͬѧ����һ����ѧ��ҵ����ͬһ��ֱ������ϵ�л����ĸ�����������ͼ��ʹ���ǵĵ����ֱ�Ϊ$\sqrt{3}$��$\frac{1}{10}$��e��$\frac{3}{5}$��ʱ��ͬѧΪ�˺�ĺ��ͬѧ��ȥ�棬�ʴ�Ӣͬѧ������ҵ���ܿ�ͳ����ˣ������ͼ���ڶ��죬ŷ����ʦ��������ʱ��ͬѧ�����㻭�����������У������ǵ���Ϊe�Ķ�������ͼ��ʱ��ͬѧ�����Զԣ��������ͨ�죮�ۿ�ʱ��ͬѧ��Ҫ��ŷ����ʦѵ��һ����������ǵ����ܲ��ܰ���һ�ѣ��ش���������أ�
ŷ����ʦ���ø�ʱ��ͬѧ����һ����ѧ��ҵ����ͬһ��ֱ������ϵ�л����ĸ�����������ͼ��ʹ���ǵĵ����ֱ�Ϊ$\sqrt{3}$��$\frac{1}{10}$��e��$\frac{3}{5}$��ʱ��ͬѧΪ�˺�ĺ��ͬѧ��ȥ�棬�ʴ�Ӣͬѧ������ҵ���ܿ�ͳ����ˣ������ͼ���ڶ��죬ŷ����ʦ��������ʱ��ͬѧ�����㻭�����������У������ǵ���Ϊe�Ķ�������ͼ��ʱ��ͬѧ�����Զԣ��������ͨ�죮�ۿ�ʱ��ͬѧ��Ҫ��ŷ����ʦѵ��һ����������ǵ����ܲ��ܰ���һ�ѣ��ش���������أ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com