
已知 ,
, ,直线
,直线 与函数
与函数 、
、 的图象都相切,且与函数
的图象都相切,且与函数 的图象的切点的横坐标为
的图象的切点的横坐标为 .
.
(Ⅰ)求直线 的方程及
的方程及 的值;
的值;
(Ⅱ)若 (其中
(其中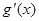 是
是 的导函数),求函数
的导函数),求函数 的最大值;
的最大值;
(Ⅲ)当 时,求证:
时,求证: .
.
(Ⅰ)直线 的方程为
的方程为 .
. .
.
(Ⅱ)当 时,
时, 取最大值,其最大值为2.
取最大值,其最大值为2.
(Ⅲ)
解析试题分析:(Ⅰ) ,
, .∴直线
.∴直线 的斜率为
的斜率为 ,且与函数
,且与函数 的图象的切点坐标为
的图象的切点坐标为 . ∴直线
. ∴直线 的方程为
的方程为 . 又∵直线
. 又∵直线 与函数
与函数 的图象相切,
的图象相切,
∴方程组 有一解. 由上述方程消去
有一解. 由上述方程消去 ,并整理得
,并整理得 ①
①
依题意,方程①有两个相等的实数根,
解之,得 或
或

 .
.
(Ⅱ)由(Ⅰ)可知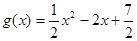 ,
,
 .
.  .
.
∴当 时,
时, ,当
,当 时,
时, .
.
∴当 时,
时, 取最大值,其最大值为2.
取最大值,其最大值为2.
(Ⅲ)  .
.  ,
,  ,
,  .
.
由(Ⅱ)知当 时,
时, ∴当
∴当 时,
时, ,
, . ∴
. ∴
考点:导数的几何意义,直线方程,利用导数研究函数的极值(最值),不等式证明问题。
点评:典型题,切线的斜率,等于在切点的导函数值。利用导数研究函数的极值,一般遵循“求导数、求驻点、研究导数的正负、确定极值”,利用“表解法”,清晰易懂。不等式的证明问题,往往通过构造函数,通过研究函数的最值达到目的。


科目:高中数学 来源: 题型:解答题
已知函数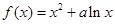 的图象在点
的图象在点 处的切线斜率为
处的切线斜率为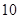 .
.
(Ⅰ)求实数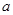 的值;
的值;
(Ⅱ)判断方程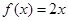 根的个数,证明你的结论;
根的个数,证明你的结论;
(Ⅲ)探究:是否存在这样的点 ,使得曲线
,使得曲线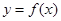 在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com