
如图,F1,F2是双曲线C: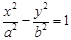 (a>0,b>0) 的左、右焦点,过F1的直线与
(a>0,b>0) 的左、右焦点,过F1的直线与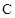 的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3 : 4 : 5,则双 曲线的离心率为 .
的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3 : 4 : 5,则双 曲线的离心率为 .
解析试题分析:根据双曲线的定义可求得a=1,∠ABF2=90°,再利用勾股定理可求得2c=|F1F2|,从而可求得双曲线的离心率.
解:∵|AB|:|BF2|:|AF2|=3:4:5,不妨令|AB|=3,|BF2|=4,|AF2|=5,∵|AB|2+|BF2|2=|AF2|2,∴∠ABF2=90°,又由双曲线的定义得:|BF1|-|BF2|=2a,|AF2|-|AF1|=2a,∴|AF1|+3-4=5-|AF1|,∴|AF1|=3.∴|BF1|-|BF2|=3+3-4=2a,
∴a=1.在Rt△BF1F2中,|F1F2|2=|BF1|2+|BF2|2=62+42=52,∵|F1F2|2=4c2,∴4c2=52,∴c=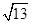 ,∴双曲线的离心率
,∴双曲线的离心率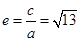 ,故答案为
,故答案为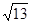 。
。
考点:双曲线的简单性质
点评:本题考查双曲线的简单性质,考查转化思想与运算能力,求得a与c的值是关键,属于中档题.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com