练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某单位将举办庆典活动，要在广场上竖立一形状为等腰梯形的彩门BADC （如图），设计要求彩门的面积为S （单位：m2）高为h（单位：m）（S，h为常数），彩门的下底BC固定在广场地面上，上底和两腰由不锈钢支架构成，设腰和下底的夹角为α，不锈钢支架的长度和记为l．
    （1）请将l表示成关于α的函数l=f（α）；
    （2）问当α为何值时l最小？并求最小值．

    【答案】
    （1）解：设上底长为a，则S= ，

    ∴a= ﹣ ，

    ∴l= ﹣ + （0＜α＜ ）


    （2）解：l′=h ，

    ∴0＜α＜ ，l′＜0， ＜α＜ ，l′＞0，

    ∴ 时，l取得最小值 m


    【解析】（1）求出上底，即可将l表示成关于α的函数l=f（α）；（2）求导数，取得函数的单调性，即可解决当α为何值时l最小？并求最小值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知圆： 和点，动圆经过点且与圆相切，圆心的轨迹为曲线．

    （1）求曲线的方程；

    （2）点是曲线与轴正半轴的交点，点， 在曲线上，若直线， 的斜率分别是， ，满足，求面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月5日的昼夜温差与实验室每天每100颗种子中的发芽数，得到如下资料：

    日期

    12月1日

    12月2日

    12月3日

    12月4日

    12月5日

    温差x(℃)

    10

    11

    13

    12

    8

    发芽数y(颗)

    23

    25

    30

    26

    16

    该农科所确定的研究方案是：先从这5组数据中选取2组，用剩下的3组数据求回归方程，再对被选取的2组数据进行检验．

    (1)求选取的2组数据恰好是不相邻的2天数据的概率；

    (2)若选取的是12月1日与12月5日的两组数据，请根据12月2日至12月4日的数据，求y关于x的线性回归方程

    (3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2颗，则认为得到的线性回归方程是可靠的，试问(2)中所得的线性回归方程是否可靠？

    (附：对于一组数据(x1，y1)，(x2，y2)，…，(xn，yn)，其回归直线的斜率和截距的最小二乘估计分别为

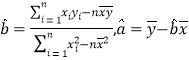
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列四个命题中正确的是（ ）.

    ①若一个平面内的两条直线与另一个平面都平行，那么这两个平面互相平行；

    ②若一条直线和两个平行平面中的一个平面垂直，那么这条直线也和另一个平面垂直；

    ③若一条直线和两个互相垂直的平面中的一个平面垂直，那么这条直线一定平行于另一个平面；

    ④若两个平面垂直，那么，一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.

    A. ②和④ B. ②和③ C. ③和④ D. ①和②

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若满足，求：

    （1）的最小值；

    （2）的范围；

    （3）的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，如图， ，图中的一系列圆是圆心分别为， 的两组同心圆，每组同心圆的半径依次为， ， ，

    按“加”依次递增，点是某两圆的一个交点，设：

    以， 为焦点，且过点的椭圆为；

    以， 为焦点，且过点的双曲线为，

    则

    （）双曲线离心率__________．

    （）若以为轴正方向，线段中点为坐标原点建立平面直角坐标系，则

    椭圆方程为__________．

    （3）双曲线渐近线方程为__________．

    （4）在两组同心圆的交点中，在椭圆上的点共__________个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

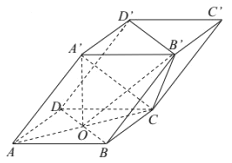
    【题目】如图，四棱柱的底面是菱形， ， ， ．

    （Ⅰ）证明：平面平面；

    （Ⅱ）若，直线上是否存在点，使得与平面所成角的正弦值为.若存在，求的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列｛an｝的首项（a是常数），（）.

    （1）求，，，并判断是否存在实数a使成等差数列.若存在，求出的通项公式；若不存在，说明理由；

    （2）设，（），为数列的前n项和，求

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若对任意的，存在实数，使恒成立，则实数的最大值为__________．

    查看答案和解析>>

    同步练习册答案