
【题目】若对任意的![]() ,存在实数
,存在实数![]() ,使
,使![]() 恒成立,则实数
恒成立,则实数![]() 的最大值为__________.
的最大值为__________.
【答案】9
【解析】分析:对任意的x∈[1,5],存在实数a,使![]() 恒成立,
恒成立,![]() .令f(x)=
.令f(x)=![]() +a,x∈[1,4].(b>0).f′(x)=1﹣
+a,x∈[1,4].(b>0).f′(x)=1﹣![]() =
=![]() =
=![]() .对b分类讨论,利用导数研究函数的单调性极值与最值即可得出.
.对b分类讨论,利用导数研究函数的单调性极值与最值即可得出.
详解:对任意的![]() ,存在实数
,存在实数![]() ,使
,使![]() 恒成立,
恒成立,
即![]()
令f(x)=![]() +a,x∈[1,4].(b>0).
+a,x∈[1,4].(b>0).
f′(x)=1﹣![]() =
=![]() =
=![]() .
.
对b分类讨论:
![]() ≥4时,函数f(x)在x∈[1,4]上单调递减:f(1)=1+a+b
≥4时,函数f(x)在x∈[1,4]上单调递减:f(1)=1+a+b![]() ,f(4)=4+
,f(4)=4+![]() +a
+a![]() ,即
,即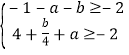 ,解得
,解得![]() ,舍去.
,舍去.
1<![]() <4时,函数f(x)在x∈[1,
<4时,函数f(x)在x∈[1,![]() )上单调递减,在(
)上单调递减,在(![]() ,4]上单调递增.f(
,4]上单调递增.f(![]() )=2
)=2![]() +a=﹣2,f(4)=4+
+a=﹣2,f(4)=4+![]() +a≤2,f(1)=1+a+b≤2,
+a≤2,f(1)=1+a+b≤2,
其中必有一个取等号,解得b=9,a=﹣8.
0<![]() ≤1时,不必要考虑.
≤1时,不必要考虑.
综上可得:b的最大值为9.
故答案为:9.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某单位将举办庆典活动,要在广场上竖立一形状为等腰梯形的彩门BADC (如图),设计要求彩门的面积为S (单位:m2)高为h(单位:m)(S,h为常数),彩门的下底BC固定在广场地面上,上底和两腰由不锈钢支架构成,设腰和下底的夹角为α,不锈钢支架的长度和记为l. 
(1)请将l表示成关于α的函数l=f(α);
(2)问当α为何值时l最小?并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
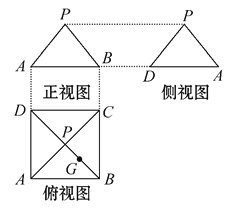
(1)根据三视图,画出该几何体的直观图.
(2)在直观图中,①证明:PD∥平面AGC;
②证明:平面PBD⊥平面AGC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组.现要从中抽取10名学生,各组内抽取的编号按依次增加10进行系统抽样.
(1)若抽出的一个号码为22,则此号码所在的组数是多少?据此写出所有被抽出学生的号码;
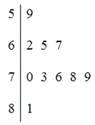
(2)分别统计这10名学生的数学成绩,获得成绩数据的茎叶图如图4所示,求该样本的方差;
(3)在(2)的条件下,从这10名学生中随机抽取两名成绩不低于73分的学生,求被抽取到的两名学生的成绩之和不小于154分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过两点
过两点![]() ,
, ![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(Ⅱ)直线![]() 过点
过点![]() 且与圆
且与圆![]() 有两个不同的交点
有两个不同的交点![]() ,
, ![]() ,若直线
,若直线![]() 的斜率
的斜率![]() 大于0,求
大于0,求![]() 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,是否存在直线![]() 使得弦
使得弦![]() 的垂直平分线过点
的垂直平分线过点![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两圆![]() ,
, ![]() 的圆心分别为c1,c2,,P为一个动点,且
的圆心分别为c1,c2,,P为一个动点,且![]() .
.
(1)求动点P的轨迹方程;
(2)是否存在过点A(2,0)的直线l与轨迹M交于不同的两点C,D,使得C1C=C1D?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆心为
,圆心为![]() ,定点
,定点![]() ,
, ![]() 为圆
为圆![]() 上一点,线段
上一点,线段![]() 上一点
上一点![]() 满足
满足![]() ,直线
,直线![]() 上一点
上一点![]() ,满足
,满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)![]() 为坐标原点,
为坐标原点, ![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与
与![]() 相切,并与轨迹
相切,并与轨迹![]() 交于不同的两点
交于不同的两点![]() .当
.当![]() 且满足
且满足![]() 时,求
时,求![]() 面积
面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com