
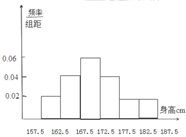
 ��1��ijʡ������������ͳ�Ƶ���������ʾ��ȫʡ100000�����������߷�����̬�ֲ�N��170.5��16���ִӸ�ʡijУ�����꼶�����������ȡ50���������ߣ��������ֱ���ѧ������ȫ������157.5cm��187.5cm֮�䣬��������������·�ʽ�ֳ�6�飺��һ��[157.5��162.5]�ڶ���[162.5��167.5]������6��[182.5��187.5]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��
��1��ijʡ������������ͳ�Ƶ���������ʾ��ȫʡ100000�����������߷�����̬�ֲ�N��170.5��16���ִӸ�ʡijУ�����꼶�����������ȡ50���������ߣ��������ֱ���ѧ������ȫ������157.5cm��187.5cm֮�䣬��������������·�ʽ�ֳ�6�飺��һ��[157.5��162.5]�ڶ���[162.5��167.5]������6��[182.5��187.5]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ������ ��1������ƽ������������ֵ��Ƶ�ʣ����ɵõ����ۣ�
��2��������Ƶ�ʷֲ�ֱ��ͼ�������ʾ�����壬�����ʾ���ߣ������ʾƵ������ÿ���а�������ĸ���������Ƶ���ֲ�ֱ��ͼ���˽����ݵķֲ������֪��ÿ����ռ�ı������Ӷ������50������������177.5cm���ϣ���177.5cm����������
��3���ȸ�����̬�ֲ��Ĺ������ȫ��ǰ130����������182.5cm���ϵ�50���е�������ȷ���εĿ���ȡֵ���������ʣ����ɵõ��εķֲ�����������
��� �⣺��1������Ƶ�ʷֲ�ֱ��ͼ������У�����꼶����ƽ������Ϊ$\overline{x}$=160��0.02��5+165��0.04��5+170��0.06��5+175��0.04��5+180��0.02��5+185��0.02��5=171.5��
�����ȫ�е�ƽ��ֵ170.5����4�֣�
��2����Ƶ�ʷֲ�ֱ��ͼ֪��������Ƶ��Ϊ0.2��
������Ϊ0.2��50=10��
����50������������177.5cm���ϣ���177.5 cm��������Ϊ10�ˣ�����6�֣�
��3����P��170.5-3��4����170.5+3��4��=0.9974��
��P����182.5��=$\frac{1-0.9974}{2}$=0.0013��
��0.0013��100 000=130��
ȫʡǰ130����������182.5 cm���ϣ���50����182.5 cm���ϵ���5�ˣ�
����������ο�ȡ0��1��2������
P����=0��=$\frac{{C}_{5}^{2}}{{C}_{10}^{2}}$=$\frac{2}{9}$��P����=1��=$\frac{{C}_{5}^{1}{C}_{5}^{1}}{{C}_{10}^{2}}$=$\frac{5}{9}$��P����=2��=$\frac{{C}_{5}^{2}}{{C}_{10}^{2}}$=$\frac{2}{9}$��
��E��=0��$\frac{2}{9}$+1��$\frac{5}{9}$+2��$\frac{2}{9}$=1������12�֣�
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ��Ӧ�����⣬Ҳ��������ɢ����������������뷽��ļ������⣬���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{17}}{3}$ | B�� | $\sqrt{5}$ | C�� | $\frac{5}{3}$ | D�� | $\frac{5}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 10 | C�� | 7 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������S-ABC�У�SA=SB=SC����$��ASB=��BSC=��CSA=\frac{��}{2}$��M��N�ֱ���AB��SC���е㣮������ֱ��SM��BN���ɵĽǵ�����ֵΪ$\frac{{\sqrt{10}}}{5}$��ֱ��SM����SAC���ɽǴ�СΪ$\frac{��}{4}$��
��ͼ������S-ABC�У�SA=SB=SC����$��ASB=��BSC=��CSA=\frac{��}{2}$��M��N�ֱ���AB��SC���е㣮������ֱ��SM��BN���ɵĽǵ�����ֵΪ$\frac{{\sqrt{10}}}{5}$��ֱ��SM����SAC���ɽǴ�СΪ$\frac{��}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��������� | B�� | �۽������� | C�� | ֱ�������� | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����������ABCD-A1B1C1D1�У�����M���߶�C1D1�ϣ�E��F�ֱ�ΪAD��AB���е㣮������ֱ��ME��DF���ɵĽ�Ϊ�ȣ���sin�ȵ���СֵΪ$\frac{\sqrt{21}}{5}$��
��ͼ����������ABCD-A1B1C1D1�У�����M���߶�C1D1�ϣ�E��F�ֱ�ΪAD��AB���е㣮������ֱ��ME��DF���ɵĽ�Ϊ�ȣ���sin�ȵ���СֵΪ$\frac{\sqrt{21}}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
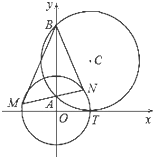 ��ͼ��ԲC��x�������ڵ�T��1��0������y�������ύ������A��B����A���Ϸ�������|AB|=2������A����һ��ֱ����ԲO��x2+y2=1�ཻ��M��N���㣬�����������ۣ�
��ͼ��ԲC��x�������ڵ�T��1��0������y�������ύ������A��B����A���Ϸ�������|AB|=2������A����һ��ֱ����ԲO��x2+y2=1�ཻ��M��N���㣬�����������ۣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com