
分析 (Ⅰ)根据偶函数的定义建立恒等式f(-x)=f(x)在R上恒成立,从而求出a的值即可;
(Ⅱ)利用题目所给的方法进行解答即可.
解答 解:(Ⅰ)∵f(x)是偶函数,∴f(-x)=f(x)在R上恒成立,
即(-x)2+|-x-a|+1=x2+|x-a|+1,
化简整理,得ax=0在R上恒成立,
∴a=0
(Ⅱ)因为函数g(x)=-x2+mx+1是区间[-1,1]上的平均值函数,
所以存在x0∈(-1,1),使$\frac{g(1)-g(-1)}{1-(-1)}$=g(x0),
而$\frac{g(1)-g(-1)}{1-(-1)}$=m,存在x0∈(-1,1),使得g(x0)=m,
亦即关于x方程-x2+mx+1=m在(-1,1)有解
由-x2+mx+1-m在=0解得x1=1,x2=m-1,所以必有-<m-1<1
即0<m<2.
所以m取值范围是(0,2).
点评 本题主要考查了函数奇偶性的应用,阅读题目的能力,计算的能力,属于综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
| f(1)=-1 | f(1.25)=-0.4031 | f(1.375)=-0.1117 |
| f(1.4375)=0.0326 | f(1.5)=0.1761 | f(2)=1.3010 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
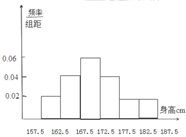 (1)某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16)现从该省某校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5]第二组[162.5,167.5],…第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.
(1)某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16)现从该省某校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5]第二组[162.5,167.5],…第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等腰三角形或直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,点E、F分别为棱长为2$\sqrt{2}$的正方体ABCD-A1B1C1D1的棱AB,C1D1的中点,点P在EF上,过点P作直线l,使得l⊥EF,且l∥平面ACD1,直线l与正方体的表面相交于M、N两点,当点P由E运动到点F时,记EP=x,△EMN的面积为f(x),则y=f(x)的图象是( )
如图所示,点E、F分别为棱长为2$\sqrt{2}$的正方体ABCD-A1B1C1D1的棱AB,C1D1的中点,点P在EF上,过点P作直线l,使得l⊥EF,且l∥平面ACD1,直线l与正方体的表面相交于M、N两点,当点P由E运动到点F时,记EP=x,△EMN的面积为f(x),则y=f(x)的图象是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com