
【题目】已知函数 ![]()
![]() ( m 为常数).
( m 为常数).
(Ⅰ)若曲线 y f x 在点 0, f 0 处的切线斜率为 1 ,求实数 m 的值.
(Ⅱ)求函数 f x 的极值.
(Ⅲ)证明:当 x 0 时,![]() .
.
【答案】(1)m = 2 ;(2)f (x)的极小值为![]() ,无极大值;(3)证明见解析.
,无极大值;(3)证明见解析.
【解析】
(Ⅰ)求出f′(x)=ex﹣m,(m∈R),f′(0)=1﹣m,利用导数的几何意义能求出m;(Ⅱ)由f′(x)=ex﹣m,(m∈R),函数f(x)定义域为(﹣∞,+∞),利用导数性质能求出f(x)的极值;(Ⅲ)设函数g(x)=ex﹣x2,则g′(x)=ex﹣2x,当m=2时,g′(x)=f(x)≥f(ln2),由g′(x)>0恒成立,能证明ex>x2.
(Ⅰ)∵函数f(x)=ex﹣mx(m为常数),
∴f′(x)=ex﹣m,(m∈R),∴f′(0)=1﹣m,
∵曲线y=f(x)在点(0,f(0))的切线斜率为﹣1,
∴f′(0)=1﹣m=﹣1,
解得m=2.
(Ⅱ)∵f′(x)=ex﹣m,(m∈R),
函数f(x)定义域为(﹣∞,+∞),
当m≤0时,f′(x)>0,函数f(x)在(﹣∞,+∞)上单调递增,
此时没有极值;
当m>0时,令f′(x)=0,解得x=lnm,
则随着x的变化,f′(x),f(x)变化如下表:
x | (﹣∞,lnm) | lnm | (lnm,+∞) |
f′(x) | ﹣ | 0 | + |
f(x) | ↓ | 极小值 | ↑ |
由上表知函数f(x)在(lnm,+∞)上单调递增,在(﹣∞,lnm)上单调递减,
则在x=lnm处取得极小值f(lnm)=elnm﹣mlnm=m(1﹣lnm),
无极大值.
证明:(Ⅲ)设函数g(x)=ex﹣x2,
则g′(x)=ex﹣2x,
由(Ⅱ)知m=2时,g′(x)=f(x)≥f(ln2),
∵f(ln2)=2(1﹣ln2)>0,∴g′(x)>0恒成立,
即函数g(x)在R上递增,
∵g(0)=1,∴当x>0时,g(x)>g(0)>0,
∴ex>x2.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】某校高一(1)(2)两个班联合开展“诗词大会进校园,国学经典润心田”古诗词竞赛主题班会活动,主持人从这两个班分别随机选出20名同学进行当场测试,他们的测试成绩按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)分组,分别用频率分布直方图与茎叶图统计如图(单位:分): 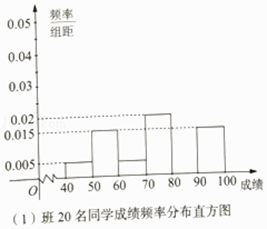
高一(2)班20名学生成绩茎叶图:
4 | 5 |
5 | 2 |
6 | 4 5 6 8 |
7 | 0 5 5 8 8 8 8 9 |
8 | 0 0 5 5 |
9 | 4 5 |
(Ⅰ)分别计算两个班这20名同学的测试成绩在[80,90)的频率,并补全频率分布直方图;
(Ⅱ)分别从两个班随机选取1人,设这两人中成绩在[80,90)的人数为X,求X的分布列(频率当作概率使用).
(Ⅲ)运用所学统计知识分析比较两个班学生的古诗词水平.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具所需成本费用为P元,且P=1 000+5x+![]() x2,而每套售出的价格为Q元,其中Q(x)=a+
x2,而每套售出的价格为Q元,其中Q(x)=a+![]() (a,b∈R),
(a,b∈R),
(1)问:玩具厂生产多少套时,使得每套所需成本费用最少?
(2)若生产出的玩具能全部售出,且当产量为150套时利润最大,此时每套价格为30元,求a,b的值.(利润=销售收入-成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定实数 t,已知命题 p:函数![]() 有零点;命题 q: x∈[1,+∞)
有零点;命题 q: x∈[1,+∞) ![]() ≤4
≤4![]() -1.
-1.
(Ⅰ)当 t=1 时,判断命题 q 的真假;
(Ⅱ)若 p∨q 为假命题,求 t 的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查高一新生中女生的体重情况,校卫生室随机选20名女生作为样本,测量她们的体重(单位:kg),获得的所有数据按照区间![]() ,
, ![]() ,
, ![]() ,
, ![]() 进行分组,得到频率分布直方图如图所示,已知样本中体重在区间
进行分组,得到频率分布直方图如图所示,已知样本中体重在区间![]() 上的女生数与体重在区间
上的女生数与体重在区间![]() 上的女生数之比为
上的女生数之比为![]() .
.

(1)求![]() 的值;
的值;
(2)从样本中体重在区间![]() 上的女生中随机抽取两人,求体重在区间
上的女生中随机抽取两人,求体重在区间![]() 上的女生至少有一人被抽中的概率.
上的女生至少有一人被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年入冬以来,各地雾霾天气频发,![]() 频频爆表(
频频爆表(![]() 是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与
是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与![]() 的浓度是否相关,某市现采集周一到周五某一时间段车流量与
的浓度是否相关,某市现采集周一到周五某一时间段车流量与![]() 的数据如下表:
的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 69 | 70 | 74 | 78 | 79 |
(1)请根据上述数据,在下面给出的坐标系中画出散点图;

(2)试判断![]() 与
与![]() 是否具有线性关系,若有请求出
是否具有线性关系,若有请求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,若没有,请说明理由;
,若没有,请说明理由;
(3)若周六同一时间段的车流量为60万辆,试根据(2)得出的结论,预报该时间段的![]() 的浓度(保留整数).
的浓度(保留整数).
参考公式:
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;②用相关指数可以刻画回归的效果,值越小说明模型的拟合效果越好;③比较两个模型的拟合效果,可以比较残差平方和大小,残差平方和越小的模型拟合效果越好.其中说法正确的是( )
A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知过点![]() 的直线
的直线![]() 的参数方程是
的参数方程是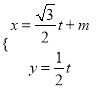 (
(![]() 为参数).以平面直角坐标系的原点为极点,
为参数).以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程式为
的极坐标方程式为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com