已知函数f(x)=x|x-a|-lnx.
(1)若a=1,求函数f(x)在区间[1,e]的最大值;
(2)求函数f(x)的单调区间;
(3)若f(x)>0恒成立,求a的取值范围.
解:(1)若a=1,则f(x)=x|x-1|-lnx.
当x∈[1,e]时,f(x)=x
2-x-lnx,

,
所以f(x)在[1,e]上单调增,
∴

.
(2)由于f(x)=x|x-a|-lnx,x∈(0,+∞).
(ⅰ)当a≤0时,则f(x)=x
2-ax-lnx,

,
令f′(x)=0,得

(负根舍去),
且当x∈(0,x
0)时,f′(x)<0;当x∈(x
0,+∞)时,f′(x)>0,
所以f(x)在

上单调递减,在

上单调递增.
(ⅱ)当a>0时,
①当x≥a时,

,
令f′(x)=0,得

(

舍),
若

,即a≥1,则f′(x)≥0,
所以f(x)在(a,+∞)上单调增;
若

,即0<a<1,则当x∈(0,x
1)时,f′(x)<0;当x∈(x
1,+∞)时,f′(x)>0,
所以f(x)在区间

上是单调减,在

上单调增.
②当0<x<a时,

,
令f′(x)=0,得-2x
2+ax-1=0,记△=a
2-8,
若△=a
2-8≤0,即
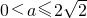
,则f′(x)≤0,
故f(x)在(0,a)上单调减;
若△=a
2-8>0,即
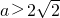
,
则由f′(x)=0得

,

,且0<x
3<x
4<a,
当x∈(0,x
3)时,f′(x)<0;当x∈(x
3,x
4)时,f′(x)>0;当x∈(x
4,+∞)时,f′(x)>0,
所以f(x)在区间

上是单调减,在
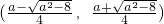
上单调增;在

上单调减.
综上所述,当a<1时,f(x)的单调递减区间是

,单调递增区间是

;
当

时,f(x)单调递减区间是(0,a),单调的递增区间是(a,+∞);
当
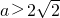
时,f(x)单调递减区间是(0,

)和

,单调的递增区间是
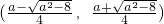
和(a,+∞).
(3)函数f(x)的定义域为x∈(0,+∞).
由f(x)>0,得

.*
(ⅰ)当x∈(0,1)时,|x-a|≥0,

,不等式*恒成立,所以a∈R;
(ⅱ)当x=1时,|1-a|≥0,
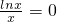
,所以a≠1;
(ⅲ)当x>1时,不等式*恒成立等价于

恒成立或

恒成立.
令

,则

.
因为x>1,所以h'(x)>0,从而h(x)>1.
因为

恒成立等价于a<(h(x))
min,所以a≤1.
令

,则

.
再令e(x)=x
2+1-lnx,则

在x∈(1,+∞)上恒成立,e(x)在x∈(1,+∞)上无最大值.
综上所述,满足条件的a的取值范围是(-∞,1).
分析:(1)当a=1时,利用导数可判断f(x)在[1,e]上的单调性,由单调性即可求得其最大值;
(2)求出f(x)的定义域,先按(ⅰ)a≤0,(ⅱ)a>0两种情况进行讨论,其中a>0时讨论去绝对值符号,利用导数符号即可判断单调性;
(3)函数f(x)的定义域为x∈(0,+∞),f(x)>0,即

.根据

的符号对x进行分类讨论:x∈(0,1)时,当x=1时,当x>1时,其中x>1时去掉绝对值符号转化为求函数最值即可解决.
点评:本题考查利用导数研究函数的单调性、求函数在闭区间上的最值及函数恒成立问题,考查分类讨论思想,考查学生分析问题解决问题的能力,综合性强,难度大,对能力要求较高.

 ,
, .
. ,
, (负根舍去),
(负根舍去), 上单调递减,在
上单调递减,在 上单调递增.
上单调递增. ,
, (
( 舍),
舍), ,即a≥1,则f′(x)≥0,
,即a≥1,则f′(x)≥0, ,即0<a<1,则当x∈(0,x1)时,f′(x)<0;当x∈(x1,+∞)时,f′(x)>0,
,即0<a<1,则当x∈(0,x1)时,f′(x)<0;当x∈(x1,+∞)时,f′(x)>0, 上是单调减,在
上是单调减,在 上单调增.
上单调增. ,
,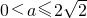 ,则f′(x)≤0,
,则f′(x)≤0,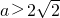 ,
, ,
, ,且0<x3<x4<a,
,且0<x3<x4<a, 上是单调减,在
上是单调减,在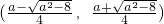 上单调增;在
上单调增;在 上单调减.
上单调减. ,单调递增区间是
,单调递增区间是 ;
; 时,f(x)单调递减区间是(0,a),单调的递增区间是(a,+∞);
时,f(x)单调递减区间是(0,a),单调的递增区间是(a,+∞);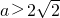 时,f(x)单调递减区间是(0,
时,f(x)单调递减区间是(0, )和
)和 ,单调的递增区间是
,单调的递增区间是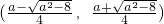 和(a,+∞).
和(a,+∞). .*
.* ,不等式*恒成立,所以a∈R;
,不等式*恒成立,所以a∈R;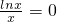 ,所以a≠1;
,所以a≠1;  恒成立或
恒成立或 恒成立.
恒成立. ,则
,则 .
. 恒成立等价于a<(h(x))min,所以a≤1.
恒成立等价于a<(h(x))min,所以a≤1. ,则
,则 .
. 在x∈(1,+∞)上恒成立,e(x)在x∈(1,+∞)上无最大值.
在x∈(1,+∞)上恒成立,e(x)在x∈(1,+∞)上无最大值. .根据
.根据 的符号对x进行分类讨论:x∈(0,1)时,当x=1时,当x>1时,其中x>1时去掉绝对值符号转化为求函数最值即可解决.
的符号对x进行分类讨论:x∈(0,1)时,当x=1时,当x>1时,其中x>1时去掉绝对值符号转化为求函数最值即可解决.

 名校课堂系列答案
名校课堂系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<