
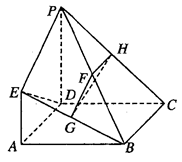
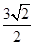 .
.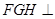 平面
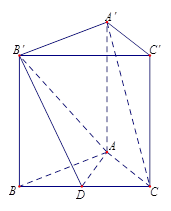
平面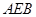 ,证明面面垂直,先证线面垂直,即证一个平面过另一个平面的垂线,注意到F,H分别为线段PB,PC的中点,所以FH∥BC,只要CB⊥平面
,证明面面垂直,先证线面垂直,即证一个平面过另一个平面的垂线,注意到F,H分别为线段PB,PC的中点,所以FH∥BC,只要CB⊥平面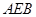 ,则FH⊥平面
,则FH⊥平面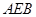 ,由已知EA⊥平面ABCD,则EA⊥CB,而四边形ABCD是正方形,CB⊥AB,从而可得CB⊥平面
,由已知EA⊥平面ABCD,则EA⊥CB,而四边形ABCD是正方形,CB⊥AB,从而可得CB⊥平面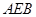 ,即可证出平面
,即可证出平面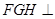 平面
平面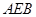 ;(Ⅱ)这是一个探索性命题,一边假设存在,作为条件,进行推理即可,有已知条件,先判断EF⊥PB(因为若EF不垂直PB,则点
;(Ⅱ)这是一个探索性命题,一边假设存在,作为条件,进行推理即可,有已知条件,先判断EF⊥PB(因为若EF不垂直PB,则点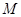 就不存在),若PB⊥平面EFM,只需使PB⊥FM,注意到三角形
就不存在),若PB⊥平面EFM,只需使PB⊥FM,注意到三角形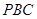 是一个直角三角形,这样△PFM∽△PCB,利用线段比例关系,可得PM=
是一个直角三角形,这样△PFM∽△PCB,利用线段比例关系,可得PM=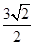 ,从得结论.
,从得结论.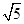 ,
,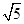 ,所以PE=BE.
,所以PE=BE.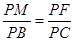 , 11分
, 11分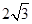 ,PF=
,PF=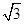 ,PC=
,PC=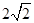 ,所以PM=
,所以PM=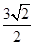 ..12分
..12分

 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
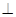 平面
平面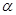 ,直线
,直线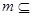 平面
平面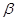 ,则下列四个结论:
,则下列四个结论: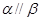 ,则
,则 ②若
②若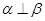 ,则
,则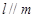
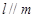 ,则
,则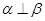 ④若
④若 ,则
,则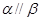
| A.①④ | B.②④ | C.①③ | D.②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
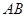 是
是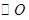 的直径,
的直径,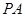 垂直于
垂直于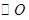 所在的平面,
所在的平面,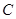 是圆周上不同于
是圆周上不同于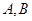 的任意一点,则图中直角三角形有 个.(要求:只需填直角三角形的个数,不需要具体指出三角形名称).
的任意一点,则图中直角三角形有 个.(要求:只需填直角三角形的个数,不需要具体指出三角形名称).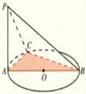
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
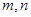 与平面
与平面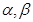 ,有下列四个命题:
,有下列四个命题: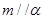 ,
,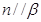 ,且
,且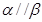 ,则
,则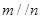 ;
;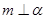 ,
,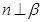 ,且
,且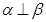 ,则
,则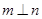 ;
;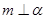 ,
,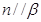 ,且
,且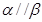 ,则
,则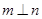 ;
;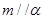 ,
,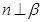 ,且
,且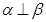 ,则
,则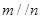 ;
;| A.①② | B.③④ | C.②③ | D.①④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com