【题目】为了了解某班学生的会考合格率，要从该班70人中选30人进行考察分析，则70人的会考成绩的全体是______，样本是______，样本量是______.
科目：高中数学 来源： 题型：
【题目】已知椭圆
的两个焦点与短轴的一个端点是等边三角形的三个顶点，且长轴长为4.
（1）求椭圆
的方程；
（2）若
是椭圆
的左顶点，经过左焦点
的直线
与椭圆
交于
，
两点，求
与
的面积之差的绝对值的最大值.（
为坐标原点）
查看答案和解析>>
科目：高中数学 来源： 题型：
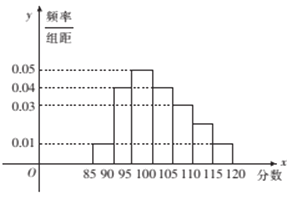
【题目】某校高二奥赛班
名学生的物理测评成绩（满分120分）分布直方图如下，已知分数在100-110的学生数有21人．
（1）求总人数
和分数在110-115分的人数
；
（2）现准备从分数在110-115的
名学生（女生占
）中任选3人，求其中恰好含有一名女生的概率；
（3）为了分析某个学生的学习状态，对其下一阶段的学生提供指导性建议，对他前7次考试的数学成绩
（满分150分），物理成绩
进行分析，下面是该生7次考试的成绩．
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩与数学成绩是线性相关的，若该生的数学成绩达到130分，请你估计他的物理成绩大约是多少？
附：对于一组数据
，
……
，其回归线
的斜率和截距的最小二乘估计分别为：
，
．
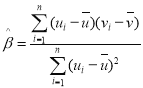查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知中心在坐标原点，焦点在
轴上的椭圆，离心率为
且过点
，过定点
的动直线与该椭圆相交于
、
两点.
（1）若线段
中点的横坐标是
，求直线
的方程；
（2）在
轴上是否存在点
，使
为常数？若存在，求出点
的坐标；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】脱贫是政府关注民生的重要任务，了解居民的实际收入状况就显得尤为重要.现从某地区随机抽取
个农户，考察每个农户的年收入与年积蓄的情况进行分析，设第
个农户的年收入
（万元），年积蓄
（万元），经过数据处理得
（Ⅰ）已知家庭的年结余
对年收入
具有线性相关关系，求线性回归方程；
（Ⅱ）若该地区的农户年积蓄在
万以上，即称该农户已达小康生活，请预测农户达到小康生活的最低年收入应为多少万元？
附：在
中， 
其中
为样本平均值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中， 
底面
，底面
是直角梯形， 
．
（1）在
上确定一点
，使得
平面
，并求
的值；
（2）在（1）条件下，求平面
与平面
所成锐二面角的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点
是圆
上任意一点（
是圆心），点
与点
关于原点对称．线段
的中垂线
分别与
交于
两点．
（1）求点
的轨迹
的方程；
（2）直线经过
，与抛物线
交于
两点，与
交于
两点．当以
为直径的圆经过
时，求
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
将圆
上每一点的纵坐标保持不变，横坐标变为原来的2倍得到曲线
．
（1）写出曲线
的参数方程；
（2）以坐标原点为极点，
轴正半轴为极轴坐标建立极坐标系，已知直线
的极坐标方程为
，若
分别为曲线
和直线
上的一点，求
的最近距离．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
