
 ij��̬ũׯ������ƽ��ͼΪ����ABCD����֪AB=4��BC=10��EΪAD��һ�㣬��AE=2��PΪ������һ��ʱͣ���㣬��P��AB��BC�ľ����Ϊ3��EC��EBΪ�����ϸ��ţ�Ϊ�˹̶����ţ�����������ʱͣ����P�ټ���һ������MN������M��N�ֱ��Ǹ���EC��EB�ϵ㣮�����ſ��ȡ��������߿��Ȳ��ƣ�����EM=d��
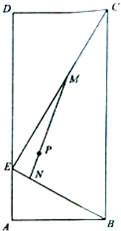
ij��̬ũׯ������ƽ��ͼΪ����ABCD����֪AB=4��BC=10��EΪAD��һ�㣬��AE=2��PΪ������һ��ʱͣ���㣬��P��AB��BC�ľ����Ϊ3��EC��EBΪ�����ϸ��ţ�Ϊ�˹̶����ţ�����������ʱͣ����P�ټ���һ������MN������M��N�ֱ��Ǹ���EC��EB�ϵ㣮�����ſ��ȡ��������߿��Ȳ��ƣ�����EM=d������ ��1����EΪ����ԭ�㣬AD����ֱ��Ϊy�ᣬ��E��ֱ��AD��ֱ��Ϊx�ᣬ����ƽ��ֱ������ϵ��������õ�����꣬���ֱ��EC��EB�ķ��̣����M��N�����꣬����PΪMN �е����m��n���ɣ�
��2������P��MN�ϵõ�б����ȣ��Ӷ��õ�����m��n�ĵ�ʽ�������ڻ�������ʽ��mn����Сֵ��
��� �⣺��1����EΪ����ԭ�㣬AD����ֱ��Ϊy�ᣬ��E��ֱ��AD��ֱ��Ϊx�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵ��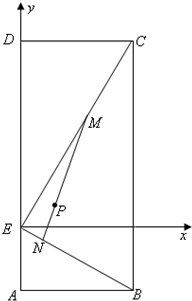 ��C��4��8����B��4��-2����P��1��1��
��C��4��8����B��4��-2����P��1��1��
��EC��y=2x EB��y=$-\frac{1}{2}$x��
��EC��EB
��M��m��2m����N��2n��n������m��0��n��0��
��PΪMN���е�
��$\left\{\begin{array}{l}{m+2n=2}\\{2m-n=2}\end{array}\right.$
��$\left\{\begin{array}{l}{m=1.2}\\{n=0.4}\end{array}\right.$ ��ʱM��1.2��2.4����d=$\frac{6\sqrt{5}}{5}$��
�𣺵�d=$\frac{6\sqrt{5}}{5}$ʱ��PΪ����MN�е㣮����7�֣�
��2����kPM=kPN
��$\frac{2m-1}{m-1}=\frac{-n-1}{2n-1}$
��m+3n=5mn��$\frac{2}{3}��m��4$��$\frac{4}{17}��n��2$��
��EC��EB
��${S}_{��EMN}=\frac{1}{2}$EM•EN=$\frac{5}{2}$mn
��m+3n=5mn$��2\sqrt{3mn}$���ҽ���m=3n=1.2ʱȡ�Ⱥţ�
��mn$��\frac{12}{25}$��
��${S}_{��EMN}=\frac{5}{2}mn$��1.2����ʱd=$\frac{6\sqrt{5}}{5}$������14�֣�
�𣺵�d=$\frac{6\sqrt{5}}{5}$ʱ��������EMN�����С����СΪ1.2������16�֣�
���� ���⿼����ֱ�߷��̡�ֱ����ֱ�ߵĽ������⡢��������ʽ����������ֵ���ؼ����ʵ��Ľ�������ϵ��ʹ�������껯��


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�1-3ln2�� | B�� | ��1��3ln2-1�� | C�� | ��1-3ln2��1�� | D�� | ��1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.97 | B�� | 0.83 | C�� | 0.32 | D�� | 0.17 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{3}$ | C�� | $\frac{2��}{3}$ | D�� | $\frac{5��}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com