
分析 将函数化为y=($\frac{1}{2}$$\sqrt{{x}^{2}+2}$+$\frac{1}{\sqrt{{x}^{2}+2}}$)+$\frac{1}{2}$$\sqrt{{x}^{2}+2}$,注意运用基本不等式和二次函数的最值,同时注意最小值取得时,x的取值要一致,即可得到所求最小值.
解答 解:函数y=$\frac{{{x^2}+3}}{{\sqrt{{x^2}+2}}}$=$\frac{{x}^{2}+2+1}{\sqrt{{x}^{2}+2}}$
=$\sqrt{{x}^{2}+2}$+$\frac{1}{\sqrt{{x}^{2}+2}}$
=($\frac{1}{2}$$\sqrt{{x}^{2}+2}$+$\frac{1}{\sqrt{{x}^{2}+2}}$)+$\frac{1}{2}$$\sqrt{{x}^{2}+2}$
≥2$\sqrt{\frac{1}{2}}$+$\frac{1}{2}\sqrt{2}$=$\frac{3\sqrt{2}}{2}$.
当且仅当$\frac{1}{2}$$\sqrt{{x}^{2}+2}$=$\frac{1}{\sqrt{{x}^{2}+2}}$,即有x=0,取得等号.
则函数的最小值为$\frac{{3\sqrt{2}}}{2}$.
故答案为:$\frac{3\sqrt{2}}{2}$.
点评 本题考查基本不等式的运用:求最值,注意求最值的条件:一正二定三等,属于中档题和易错题.


科目:高中数学 来源: 题型:解答题
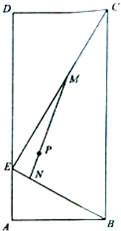 某生态农庄池塘的平面图为矩形ABCD,已知AB=4,BC=10,E为AD上一点,且AE=2,P为池塘内一临时停靠点,且P到AB,BC的距离均为3,EC,EB为池塘上浮桥,为了固定浮桥,现准备进过临时停靠点P再架设一座浮桥MN,其中M,N分别是浮桥EC,EB上点.(浮桥宽度、池塘岸边宽度不计),设EM=d,
某生态农庄池塘的平面图为矩形ABCD,已知AB=4,BC=10,E为AD上一点,且AE=2,P为池塘内一临时停靠点,且P到AB,BC的距离均为3,EC,EB为池塘上浮桥,为了固定浮桥,现准备进过临时停靠点P再架设一座浮桥MN,其中M,N分别是浮桥EC,EB上点.(浮桥宽度、池塘岸边宽度不计),设EM=d,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.2 | B. | 0.4 | C. | 0.6 | D. | 0.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 推理①②全错 | B. | 推理①对,推理②错 | C. | 推理①错,推理②对 | D. | 推理①②全对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com