
| A. | (-∞,1-3ln2) | B. | (1,3ln2-1) | C. | (1-3ln2,1) | D. | (1,+∞) |
分析 先求出函数的导数,得到函数的单调区间,结合函数的单调性得到不等式组,解出即可.
解答 解:函数f(x)的定义域为(0,+∞),
f′(x)=1+$\frac{2}{{x}^{2}}$-$\frac{3}{x}$=$\frac{{x}^{2}-3x+2}{{x}^{2}}$,
令f′(x)>0,解得:x>2或x<1,令f′(x)<0,解得:1<x<2,
∴函数f(x)在(0,1),(2,+∞)递增,在(1,2)递减,
而f(1)=-1+k,f(2)=1-3ln2+k,
要使f(x)在(0,+∞)有3个零点,
只需$\left\{\begin{array}{l}{-1+k>0}\\{1-3ln2+k<0}\end{array}\right.$,解得:1<k<3ln2-1,
故选:B.
点评 本题考查了函数的单调性、极值问题,考查导数的应用,函数的零点问题,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
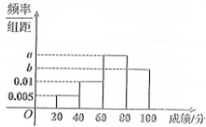 某班的全体学生(共50人)参加数学测试(百分制),成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],依此表可以估计这次测试成绩的中位数为70分.
某班的全体学生(共50人)参加数学测试(百分制),成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],依此表可以估计这次测试成绩的中位数为70分.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
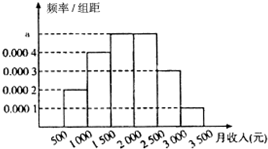 统计局就某地居民的月收入情况调查了10000人,并根据所得数据画了样本频率分布直方图,每个分组包括左端点,不包含右端点,如第一组表示收入在[500,1000).
统计局就某地居民的月收入情况调查了10000人,并根据所得数据画了样本频率分布直方图,每个分组包括左端点,不包含右端点,如第一组表示收入在[500,1000).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016×2 017 | B. | 2015×2 016 | C. | 2014×2 015 | D. | 2016×2 016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不能作出满足要求的三角形 | B. | 作出一个钝角三角形 | ||
| C. | 作出一个直角三角形 | D. | 作出一个锐角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
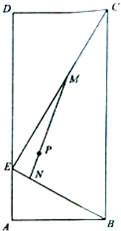 某生态农庄池塘的平面图为矩形ABCD,已知AB=4,BC=10,E为AD上一点,且AE=2,P为池塘内一临时停靠点,且P到AB,BC的距离均为3,EC,EB为池塘上浮桥,为了固定浮桥,现准备进过临时停靠点P再架设一座浮桥MN,其中M,N分别是浮桥EC,EB上点.(浮桥宽度、池塘岸边宽度不计),设EM=d,
某生态农庄池塘的平面图为矩形ABCD,已知AB=4,BC=10,E为AD上一点,且AE=2,P为池塘内一临时停靠点,且P到AB,BC的距离均为3,EC,EB为池塘上浮桥,为了固定浮桥,现准备进过临时停靠点P再架设一座浮桥MN,其中M,N分别是浮桥EC,EB上点.(浮桥宽度、池塘岸边宽度不计),设EM=d,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com