Question

【题目】如图，在四棱锥中，平面平面，，，，，，.

（1）求直线与平面所成角的正弦值.

（2）在棱上是否存在点，使得平面？若存在，求的值；若不存在，说明理由.

Answer 1

【答案】（Ⅰ ）；（Ⅱ）.

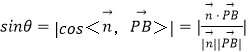【解析】分析：（Ⅰ ）取AD中点为O，连接CO，PO，由已知可得CO⊥AD，PO⊥AD．以O为坐标原点，建立空间直角坐标系，求得P（0，0，1），B（1，1，0），D（0，﹣1，0），C（2，0，0），进一步求出向量的坐标，再求出平面PCD的法向量，设PB与平面PCD的夹角为θ，由求得直线PB与平面PCD所成角的正弦值；

（Ⅱ）假设存在M点使得BM∥平面PCD，设，M（0，y1，z1），由可得M（0，1﹣λ，λ），，由BM∥平面PCD，可得

，由此列式求得当时，M点即为所求．

详解：(1)取AD的中点O，连接PO，CO.

因为PA＝PD，所以PO⊥AD.

又因为PO平面PAD，平面PAD⊥平面ABCD，

所以PO⊥平面ABCD.

因为CO平面ABCD，所以PO⊥CO.

因为AC＝CD，所以CO⊥AD.

以O为坐标原点，建立空间直角坐标系如图：

则P（0，0，1），B（1，1，0），D（0，﹣1，0），C（2，0，0），

则，，

设为平面PCD的法向量，

则由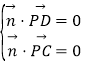，得，则．

设PB与平面PCD的夹角为θ，则=；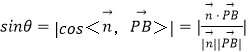

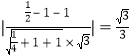(2) 假设存在M点使得BM∥平面PCD，设，M（0，y1，z1），

由（Ⅱ）知，A（0，1，0），P（0，0，1），，B（1，1，0），，

则有，可得M（0，1﹣λ，λ），

∴，

∵BM∥平面PCD，为平面PCD的法向量，

∴，即，解得．

综上，存在点M，即当时，M点即为所求．