
【题目】已知p:|x﹣a|<3(a为常数);q:代数式 ![]() 有意义.
有意义.
(1)若a=1,求使“p∧q”为真命题的实数x的取值范围;
(2)若p是q成立的充分不必要条件,求实数a的取值范围.
【答案】
(1)解:p:|x﹣a|<3等价于:﹣3<x﹣a<3即a﹣3<x<a+3;
q:代数式 ![]() 有意义等价于:
有意义等价于:
![]() ,即﹣1≤x<6
,即﹣1≤x<6
a=1时,p即为﹣2<x<4
若“p∧q”为真命题,则 ![]() ,得:﹣1≤x<4
,得:﹣1≤x<4
故a=1时,使“p∧q”为真命题的实数x的取值范围是[﹣1,4)
(2)解:记集合A={x|a﹣3<x<a+3},B={x|﹣1≤x<6}
若p是q成立的充分不必要条件,则AB,
因此: ![]() ,
,
∴2≤a≤3,故实数a的取值范围是[2,3].
【解析】(1)若a=1,分别求出p,q成立的等价条件,利用p∧q为真,求实数x的取值范围;(2)利用p是q的充分不必要条件,建立不等式关系即可求实数a的取值范围.
【考点精析】根据题目的已知条件,利用复合命题的真假的相关知识可以得到问题的答案,需要掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】某地方政府欲将一块如图所示的直角梯形ABCD空地改建为健身娱乐广场,已知AD∥BC,AD⊥AB,AD=2BC=2 ![]() 百米,AB=3百米,广场入口P在AB上,且AP=2BP,根据规划,过点P铺设两条互相垂直的笔直小路PM、PN(小路宽度不计),点M、N分别在边AD、BC上(包含端点),△PAM区域拟建为跳舞健身广场,△PBN区域拟建为儿童乐园,其他区域铺设绿化草坪,设∠APM=θ.
百米,AB=3百米,广场入口P在AB上,且AP=2BP,根据规划,过点P铺设两条互相垂直的笔直小路PM、PN(小路宽度不计),点M、N分别在边AD、BC上(包含端点),△PAM区域拟建为跳舞健身广场,△PBN区域拟建为儿童乐园,其他区域铺设绿化草坪,设∠APM=θ. 
(1)求绿化草坪面积的最大值;
(2)现拟将两条小路PN、PN进行不同风格的美化,小路PM的美化费用为每百米1万元,小路PN的美化费用为每百米2万元,试确定点M,N的位置,使得小路PM,PN的总美化费用最低,并求出最低费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“p∨q”是“p∧q”的充分不必要条件
B.样本10,6,8,5,6的标准差是3.3
C.K2是用来判断两个分类变量是否相关的随机变量,当K2的值很小时可以推定两类变量不相关
D.设有一个回归直线方程为 ![]() =2﹣1.5x,则变量x每增加一个单位,
=2﹣1.5x,则变量x每增加一个单位, ![]() 平均减少1.5个单位.
平均减少1.5个单位.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是
是 ![]() 直径,
直径, ![]() 所在的平面,
所在的平面, ![]() 是圆周上不同于
是圆周上不同于 ![]() 的动点.
的动点.
(1)证明:平面 ![]() 平面
平面 ![]() ;
;
(2)若 ![]() ,且当二面角
,且当二面角 ![]() 的正切值为
的正切值为 ![]() 时,求直线
时,求直线 ![]() 与平面
与平面 ![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一边长为6的正方形铁片,在铁片的四角各截去一个边长为x的小正方形后,沿图中虚线部分折起,做成一个无盖方盒. 
(1)试用x表示方盒的容积V(x),并写出x的范围;
(2)求方盒容积V(x)的最大值及相应x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|x2+x>0},集合B= ![]() ,则(UA)∪B=( )
,则(UA)∪B=( )
A.[0,2)
B.[﹣1,0]
C.[﹣1,2)
D.(﹣∞,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均不相等的等差数列{an}的前四项和S4=14,且a1 , a3 , a7成等比数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设Tn为数列{ ![]() }的前n项和,若Tn≤λan+1对n∈N*恒成立,求实数λ的最小值.
}的前n项和,若Tn≤λan+1对n∈N*恒成立,求实数λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD-A1B1C1D1为正方体,下面结论错误的是 ( )
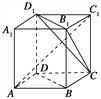
A. BD∥平面CB1D1 B. AC1⊥BD
C. AC1⊥平面CB1D1 D. 异面直线AD与CB1所成的角为60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com