练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆的离心率为，且椭圆上的一点与两个焦点构成的三角形周长为.

    （1）求椭圆的方程；

    （2）已知直线与椭圆相交于两点.

    ①若线段中点的横坐标为，求的值；

    ②在轴上是否存在点，使为定值？若是，求点的坐标；若不是，请说明理由.

    【答案】（1）；（2）①,②.

    【解析】分析：（1）先根据已知得到a,c的两个方程，解方程即得椭圆的方程.(2) ①,先联立直线与椭圆的方程得到韦达定理=2×，即得k的值. ②假设存在定点使得为定值，设点,先求，再分析得到，即得m的值.

    详解：（1）由题意得：① ，②，

    由①②解得：，∴，

    ∴椭圆的方程为.

    （2）由消去得，

    ，

    设，则，

    ①∵线段的中点的横坐标为，所以，即，

    所以；

    ②假设存在定点使得为定值，设点，

    所以

    为定值，

    即，故，

    解得：，所以当时为定值，定值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某校准备从高一年级的两个男生和三个女生中选择2个人去参加一项比赛.

    （1）若从这5个学生中任选2个人，求这2个人都是女生的概率；

    （2）若从男生和女生中各选1个人，求这2个人包括，但不包括的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直四棱柱A1B1C1D1﹣ABCD中，当底面四边形ABCD满足条件 时，有A1C⊥B1D1 ． （注：填上你认为正确的一种条件即可，不必考虑所有可能的情形．）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点的序列An(xn,0),n∈N*,其中x1=0,x2=a(a>0),A3是线段A1A2的中点,A4是线段A2A3的中点,……,An是线段An-2An-1的中点,……

    (1)写出xn与xn-1,xn-2之间的关系式(n≥3);

    (2)设an=xn+1-xn,计算a1,a2,a3,由此推测数列{an}的通项公式,并加以证明.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x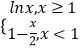）= ，若F（x）=f[f（x）+1]+m有两个零点x1 ， x2 ， 则x1x2的取值范围是（ ）
    A.[4﹣2ln2，+∞）
    B.（ ，+∞）
    C.（﹣∞，4﹣2ln2]
    D.（﹣∞， ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某机构通过对某企业今年的生产经营情况的调查，得到每月利润（单位：万元）与相应月份数的部分数据如表：

    1

    4

    7

    12

    229

    244

    241

    196

    （1）根据如表数据，请从下列三个函数中选取一个恰当的函数描述与的变化关系，并说明理由，，，；

    （2）利用（1）中选择的函数，估计月利润最大的是第几个月，并求出该月的利润.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，若在定义域内存在，使得成立，则称为函数的局部对称点．

    （1）若，证明：函数必有局部对称点；

    （2）若函数在区间内有局部对称点，求实数的取值范围；

    （3）若函数在上有局部对称点，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】记Sn为等比数列的前n项和，已知S2=2，S3=-6.

    （1）求的通项公式；

    （2）求Sn，并判断Sn+1，Sn，Sn+2是否成等差数列。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列满足，.

    （Ⅰ）证明：是等比数列；

    （Ⅱ）证明：数列中的任意三项不为等差数列；

    （Ⅲ）证明：.

    查看答案和解析>>

    同步练习册答案