
如图,四棱锥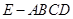 中,面
中,面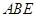
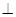 面
面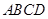 ,底面
,底面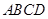 是直角梯形,侧面
是直角梯形,侧面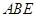 是等腰直角三角形.且
是等腰直角三角形.且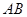 ∥
∥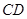 ,
,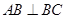 ,
,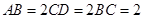 ,
,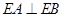 .
.
(1)判断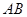 与
与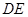 的位置关系;
的位置关系;
(2)求三棱锥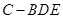 的体积;
的体积;
(3)若点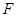 是线段
是线段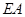 上一点,当
上一点,当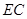 //平面
//平面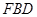 时,求
时,求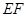 的长.
的长.
(1) ;(2)
;(2) ;(3)
;(3) .
.
解析试题分析:本题以四棱锥为几何背景考查线线垂直、线面垂直、线面平行、线线平行的判定,在解题过程中还遇到了等腰直角三角形和直角梯形以及相似三角形等基础知识,考查空间想象能力和推理论证能力.第一问,取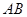 中点
中点 ,连结
,连结 ,因为
,因为 是等腰直角三角形,所以
是等腰直角三角形,所以 ,因为
,因为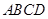 是直角梯形且
是直角梯形且 ,所以四边形
,所以四边形 为正方形,所以
为正方形,所以 ,所以
,所以 平面
平面 ,所以
,所以 ;第二问,先利用面面垂直,可得到线面垂直,得到锥体的高
;第二问,先利用面面垂直,可得到线面垂直,得到锥体的高 ,用等体积法将
,用等体积法将 转化为
转化为 ,再利用体积公式求值;第三问,先在面内找到线
,再利用体积公式求值;第三问,先在面内找到线 ,这是由于
,这是由于 // 平面
// 平面 ,再利用相似三角形,得到边长的关系,所以
,再利用相似三角形,得到边长的关系,所以 ,所以
,所以 .
.
试题解析:(1)证明:取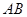 中点
中点 ,连结
,连结 ,
, .
.
因为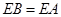 ,所以
,所以 .
.
因为四边形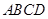 为直角梯形,
为直角梯形, ,
,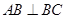 ,
,
所以四边形 为正方形,所以
为正方形,所以 .
.
所以 平面
平面 . 所以
. 所以  . 4分
. 4分
(2)由 ,面
,面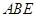
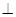 面
面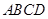 易得
易得
所以, 8分
8分
(3)解:连接 交于点,面
交于点,面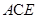
 面
面 .
.
因为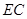 //平面
//平面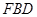 ,所以
,所以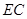 //
// .
.
在梯形 中,有
中,有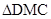 与
与 相似,
相似,
可得
所以,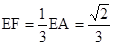 12分
12分
考点:1.线面垂直的判定定理;2.等体积法;3.相似三角形的性质.


科目:高中数学 来源: 题型:解答题
已知在直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3,D为AB的中点.
(Ⅰ)求异面直线CC1和AB的距离;
(Ⅱ)若AB1⊥A1C,求二面角A1-CD-B1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知三棱锥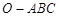 的侧棱
的侧棱 两两垂直,且
两两垂直,且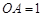 ,
,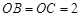 ,
,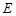 是
是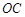 的中点。
的中点。
(1)求异面直线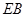 与
与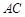 所成角的余弦值;
所成角的余弦值;
(2)求直线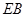 和平面
和平面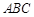 的所成角的正弦值。
的所成角的正弦值。
(3)求点E到面ABC的距离。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(如图1)在平面四边形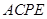 中,
中,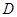 为
为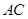 中点,
中点,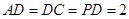 ,
,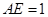 ,且
,且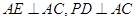 ,现沿
,现沿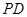 折起使
折起使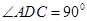 ,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.
,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.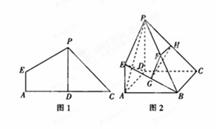
(1)求三棱锥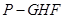 的体积;
的体积;
(2)在线段PC上是否存在一点M,使直线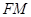 与直线
与直线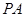 所成角为
所成角为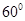 ?若存在,求出线段的长;若不存在,请说明理由.
?若存在,求出线段的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
(1)求证:PC⊥AC;
(2)求二面角M﹣AC﹣B的余弦值;
(3)求点B到平面MAC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60°的 角,AA1=2.底面ABC是边长为2的正三角形,其重心为G点,E是线段BC1上一点,且BE=3BC1.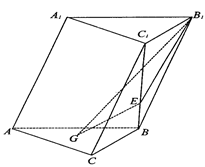

(1)求证:GE∥侧面AA1B1B;
(2)求平面B1GE与底面ABC所成锐二面角的正切值;
(3)求点B到平面B1GE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(1)如图,ABC在平面外,AB∩=P,BC∩=Q,AC∩=R,求证:P,Q,R三点共线.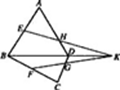
(2)如图,空间四边形ABCD中,E,F分别是AB和CB上的点,G,H分别是CD和AD上的点, 且EH与FG相交于点K. 求证:EH,BD,FG三条直线相交于同一点.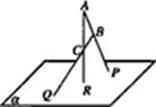
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在直三棱柱ABC-A1B1C1中,点M是A1B的中点,点N是B1C的中点,连接MN 
(Ⅰ)证明:MN//平面ABC;
(Ⅱ)若AB=1,AC=AA1=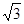 ,BC=2,求二面角A—A1C—B的余弦值的大小
,BC=2,求二面角A—A1C—B的余弦值的大小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com