
分析 (1)幂函数f(x)=${x}^{{m}^{2}-2m-3}$(m∈N*)在(0,+∞)上函数值随x的增大而减少,解得-1<m<3,由m∈N*,得m的可能取值为1,2,由其图象关于(0,0)中心对称,求出m=2,从而求出函数f(x)的解析式.
(2)由已知得$(a+1)^{-\frac{2}{3}}$<$(3-2a)^{-\frac{2}{3}}$,再由y=x-3在(-∞,0),(0,+∞)上均递减,能求出a的取值范围.
(3)由已知得g(x)=(x+4b)2-16b2,由此根据b的取值范围进行分类讨论,能求出g(x)的最小值.
解答 解:(1)∵幂函数f(x)=${x}^{{m}^{2}-2m-3}$(m∈N*)的图象关于(0,0)中心对称,且在(0,+∞)上函数值随x的增大而减少,
∴$\left\{\begin{array}{l}{{m}^{2}-2m-3是奇数}\\{{m}^{2}-2m-3<0}\end{array}\right.$,解得-1<m<3,
∵m∈N*,∴m的可能取值为1,2,
当m=1时,m2-2m-3=1-2-3=-4,不成立;
当m=2时,m2-2m-3=-3,成立,∴m=2,
∴f(x)=x-3.
(2)∵m=2,${(a+1)}^{-\frac{m}{3}}$<${(3-2a)}^{-\frac{m}{3}}$,
∴$(a+1)^{-\frac{2}{3}}$<$(3-2a)^{-\frac{2}{3}}$,
∵y=x-3在(-∞,0),(0,+∞)上均递减,
∴a+1>3-2a>0或0>a+1>3-2a或a+1<0<3-2a,
解得$\frac{2}{3}<a<\frac{3}{2}$或a<-1(不成立).
∴a的取值范围是($\frac{2}{3},\frac{3}{2}$).
(3)g(x)=$\frac{1}{x•f(x)}$+$\frac{8b}{{x}^{2}•f(x)}$=$\frac{1}{{x}^{-2}}$+$\frac{8b}{{x}^{-1}}$=x2+8bx=(x+4b)2-16b2,
∵4≤x≤16,
∴当-4b≤4,即b≥-1时,$g(x)_{min}=g(4)=(4+4b)^{2}-16{b}^{2}$=16b+16;
当4<-4b<16,即-4<b<-1时,g(x)min=g(-4b)=-16b2;
当-4b≥16,即b≤-4时,g(x)min=(16+4b)2-16b2=64b+256.
点评 本题考查函数的解析式的求法,考查实数的取值范围的求法,考查函数的最小值的求法,是中档题,解题时要注意分类讨论思想的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | 1-i | D. | 1+i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=|x|(x-4).
已知函数f(x)=|x|(x-4). 查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
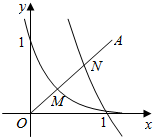 如图,点O为坐标原点,点A(1,1),若函数y=ax(a>0,且a≠1)及logbx(b>0,且b≠1)的图象与线段OA分别交于点M,N,且M,N恰好是线段OA的两个三等分点,则a,b满足( )
如图,点O为坐标原点,点A(1,1),若函数y=ax(a>0,且a≠1)及logbx(b>0,且b≠1)的图象与线段OA分别交于点M,N,且M,N恰好是线段OA的两个三等分点,则a,b满足( )| A. | a<b<1 | B. | b<a<1 | C. | b>a>1 | D. | a>b>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $k≥\frac{1}{2}$ | B. | $k≤\frac{1}{2}$ | C. | k≥$\frac{3}{5}$或k≤-$\frac{1}{2}$ | D. | -$\frac{1}{2}$≤k≤$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 150° | C. | 60° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com