
若数列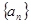 的前
的前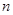 项和
项和 ,则
,则 ________________;
________________;
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数,按照点或小石子能排列的形状对数进行分类,如图2中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作 ,第2个五角形数记作
,第2个五角形数记作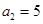 ,第3个五角形数记作
,第3个五角形数记作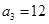 ,第4个五角形数记作
,第4个五角形数记作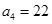 ,…,若按此规律继续下去,得数列
,…,若按此规律继续下去,得数列 ,则
,则 ;对
;对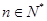 ,
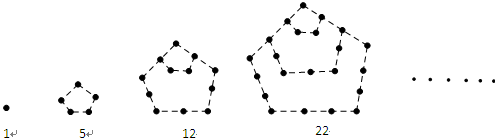
,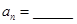 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)已知数列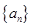 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为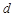 ,
, 为其前
为其前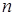 项和,且满足
项和,且满足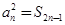 ,
,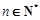 .数列
.数列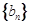 满足
满足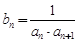 ,
,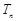 为数列
为数列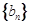 的前
的前 项和.
项和.
(1)求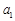 、
、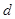 和
和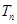 ;
;
(2)若对任意的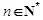 ,不等式
,不等式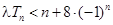 恒成立,求实数
恒成立,求实数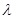 的取值范围;
的取值范围;
(3)是否存在正整数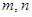
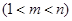 ,使得
,使得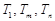 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有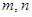 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
在数列 中,如果存在非零的常数
中,如果存在非零的常数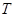 ,使
,使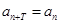 对于任意正整数
对于任意正整数 均成立,就称数列
均成立,就称数列 为周期数列,其中
为周期数列,其中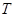 叫做数列
叫做数列 的周期. 已知数列
的周期. 已知数列 满足
满足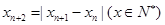 ,若
,若 ,当数列
,当数列 的周期为
的周期为 时,则数列
时,则数列 的前2012项的和为
的前2012项的和为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com