Question

15．已知平面区域D由以P（1，2）、R（3，5）、Q（-3，4）为顶点的三角形内部和边界组成．
（1）设点（x，y）在区域D内变动，求目标函数 z=2x+y的最小值；
（2）若在区域D内有无穷多个点（x，y）可使目标函数z=mx+y（m＜0）取得最小值，求m的值．

Answer 1

分析 （1）由z=2x+y得：y=-2x+z，显然直线y=-2x+z过Q（-3，4）时：z最小，代入求出即可；
（2）将目标函数z=x+my化成斜截式方程，令z=0，得到y=-mx，通过m＜0，得所求直线为和PR或QR平行的直线，判断即可．

解答 解：（1）如图示：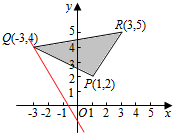
，
由z=2x+y得：y=-2x+z，
显然直线y=-2x+z过Q（-3，4）时z最小，z的最小值是：-2；
（2）依题意，令z=0，可得直线mx+y=0的斜率为：-m，
结合可行域可知当直线mx+y=0与直线PR平行时，
线段PR上的任意一点都可使目标函数z=mx+y取得最小值，
而直线PR的斜率为$\frac{3}{2}$，
所以m=-$\frac{3}{2}$．

点评 目标函数的最优解有无数多个，处理方法一般是：①将目标函数的解析式进行变形，化成斜截式②分析Z与截距的关系，是符号相同，还是相反③根据分析结果，结合图形做出结论④根据斜率相等求出参数．