
【题目】以下统计表和分布图取自《清华大学2019年毕业生就业质量报告》.
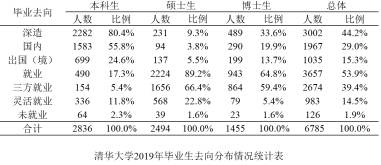
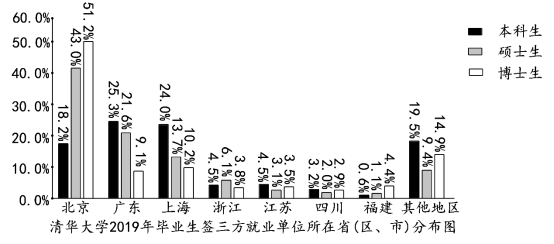
则下列选项错误的是( )
A.清华大学2019年毕业生中,大多数本科生选择继续深造,大多数硕士生选择就业
B.清华大学2019年毕业生中,硕士生的就业率比本科生高
C.清华大学2019年签三方就业的毕业生中,本科生的就业城市比硕士生的就业城市分散
D.清华大学2019年签三方就业的毕业生中,留北京人数超过一半
【答案】D
【解析】
根据统计表和分布图中的数据信息,对选项进行逐一分析判断,得出答案.
A. 根据统计表,本科生选择继续深造的比例为80.4%,硕士生选择就业的比例为89.2%,所以判断正确.
B. 根据统计表,本科生就业率17.3%, 硕士生的就业率为为89.2%.判断正确.
C. 根据分布图,签三方就业的毕业生中,硕士生的就业城市主要分布在北京、广东、上海;本科生的就业城市相对比较分散.判断正确.
D. 根据分布图, 毕业学生中,本科生人数占绝大多数,签三方就业的毕业生中,留在北京的本科生占18.2%,而硕士生和博士生分别占43.0%、51.2%,
所以毕业生留在北京的没有达到一半,所以判断错误.
故选:D


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】正态分布有极其广泛的实际背景,生产与科学实验中很多随机变量的概率分布都可以近似地用正态分布来描述.例如,同一种生物体的身长、体重等指标.随着“绿水青山就是金山银山”的观念不断的深入人心,环保工作快速推进,很多地方的环境出现了可喜的变化.为了调查某水库的环境保护情况,在水库中随机捕捞了100条鱼称重.经整理分析后发现,鱼的重量x(单位:kg)近似服从正态分布![]() ,如图所示,已知
,如图所示,已知![]() .
.
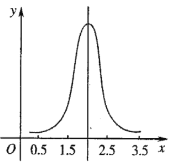
(Ⅰ)若从水库中随机捕捞一条鱼,求鱼的重量在![]() 内的概率;
内的概率;
(Ⅱ)(ⅰ)从捕捞的100条鱼中随机挑出6条鱼测量体重,6条鱼的重量情况如表.
重量范围(单位:kg) |
|
|
|
条数 | 1 | 3 | 2 |
为了进一步了解鱼的生理指标情况,从6条鱼中随机选出3条,记随机选出的3条鱼中体重在![]() 内的条数为X,求随机变量X的分布列和数学期望;
内的条数为X,求随机变量X的分布列和数学期望;
(ⅱ)若将选剩下的94条鱼称重做标记后立即放生.两周后又随机捕捞1000条鱼,发现其中带有标记的有2条.为了调整生态结构,促进种群的优化,预备捕捞体重在![]() 内的鱼的总数的40%进行出售,试估算水库中鱼的条数以及应捕捞体重在
内的鱼的总数的40%进行出售,试估算水库中鱼的条数以及应捕捞体重在![]() 内的鱼的条数.
内的鱼的条数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,直线l:x+2y=4与椭圆有且只有一个交点T.
,直线l:x+2y=4与椭圆有且只有一个交点T.
(I)求椭圆C的方程和点T的坐标;
(Ⅱ)O为坐标原点,与OT平行的直线l′与椭圆C交于不同的两点A,B,直线l′与直线l交于点P,试判断![]() 是否为定值,若是请求出定值,若不是请说明理由.
是否为定值,若是请求出定值,若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:

则下面结论中不正确的是
A. 新农村建设后,种植收入减少
B. 新农村建设后,其他收入增加了一倍以上
C. 新农村建设后,养殖收入增加了一倍
D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2012年12月18日,作为全国首批开展空气质量新标准监测的74个城市之一,郑州市正式发布![]() 数据.资料表明,近几年来,郑州市雾霾治理取得了很大成效,空气质量与前几年相比得到了很大改善.郑州市设有9个监测站点监测空气质量指数(
数据.资料表明,近几年来,郑州市雾霾治理取得了很大成效,空气质量与前几年相比得到了很大改善.郑州市设有9个监测站点监测空气质量指数(![]() ),其中在轻度污染区、中度污染区、重度污染区分别设有2,5,2个监测站点,以9个站点测得的
),其中在轻度污染区、中度污染区、重度污染区分别设有2,5,2个监测站点,以9个站点测得的![]() 的平均值为依据,播报我市的空气质量.
的平均值为依据,播报我市的空气质量.
(Ⅰ)若某日播报的![]() 为118,已知轻度污染区
为118,已知轻度污染区![]() 的平均值为74,中度污染区
的平均值为74,中度污染区![]() 的平均值为114,求重度污染区
的平均值为114,求重度污染区![]() 的平均值;
的平均值;
(Ⅱ)如图是2018年11月的30天中![]() 的分布,11月份仅有一天
的分布,11月份仅有一天![]() 在
在![]() 内.
内.
组数 | 分组 | 天数 |
第一组 |
| 3 |
第二组 |
| 4 |
第三组 |
| 4 |
第四组 |
| 6 |
第五组 |
| 5 |
第六组 |
| 4 |
第七组 |
| 3 |
第八组 |
| 1 |
①郑州市某中学利用每周日的时间进行社会实践活动,以公布的![]() 为标准,如果
为标准,如果![]() 小于180,则去进行社会实践活动.以统计数据中的频率为概率,求该校周日进行社会实践活动的概率;
小于180,则去进行社会实践活动.以统计数据中的频率为概率,求该校周日进行社会实践活动的概率;
②在“创建文明城市”活动中,验收小组把郑州市的空气质量作为一个评价指标,从当月的空气质量监测数据中抽取3天的数据进行评价,设抽取到![]() 不小于180的天数为
不小于180的天数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了更好地贯彻党的“五育并举”的教育方针,某市要对全市中小学生“体能达标”情况进行了解,决定通过随机抽样选择几个样本校对学生进行体能达标测试,并规定测试成绩低于60分为不合格,否则为合格,若样本校学生不合格人数不超过其总人数的5%,则该样本校体能达标为合格.已知某样本校共有1000名学生,现从中随机抽取40名学生参加体能达标测试,首先将这40名学生随机分为甲、乙两组,其中甲乙两组学生人数的比为3:2,测试后,两组各自的成绩统计如下:甲组的平均成绩为70,方差为16,乙组的平均成绩为80,方差为36.
(1)估计该样本校学生体能测试的平均成绩;
(2)求该样本校40名学生测试成绩的标准差s;
(3)假设该样本校体能达标测试成绩服从正态分布![]() ,用样本平均数
,用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差s作为
,用样本标准差s作为![]() 的估计值
的估计值![]() ,利用估计值估计该样本校学生体能达标测试是否合格?
,利用估计值估计该样本校学生体能达标测试是否合格?
(注:1.本题所有数据的最后结果都精确到整数;2若随机变量z服从正态分布,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在多面体![]() 中,正方形
中,正方形![]() 和矩形
和矩形![]() 互相垂直,
互相垂直,![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的中点,
的中点,![]() .
.
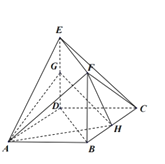
(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)在![]() 边所在的直线上存在一点
边所在的直线上存在一点![]() ,使得
,使得![]() 平面
平面![]() ,求
,求![]() 的长;
的长;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com