
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,直线l:x+2y=4与椭圆有且只有一个交点T.
,直线l:x+2y=4与椭圆有且只有一个交点T.
(I)求椭圆C的方程和点T的坐标;
(Ⅱ)O为坐标原点,与OT平行的直线l′与椭圆C交于不同的两点A,B,直线l′与直线l交于点P,试判断![]() 是否为定值,若是请求出定值,若不是请说明理由.
是否为定值,若是请求出定值,若不是请说明理由.
【答案】(I)![]() +
+![]() =1,T(1,
=1,T(1,![]() ); (Ⅱ)见解析.
); (Ⅱ)见解析.
【解析】
(I)由椭圆的离心率为![]() 得到 b2=
得到 b2=![]() a2,根据直线l:x+2y=4与椭圆有且只有一个交点T得到△=0,解得a2=4,b2=3,即得椭圆的方程. (Ⅱ)先计算出|PT|2=
a2,根据直线l:x+2y=4与椭圆有且只有一个交点T得到△=0,解得a2=4,b2=3,即得椭圆的方程. (Ⅱ)先计算出|PT|2=![]() t2,|PA|=
t2,|PA|=![]() =
=![]() |
|![]() ﹣x1|,|PB|=
﹣x1|,|PB|=![]() |
|![]() ﹣x2|,再计算
﹣x2|,再计算![]() =
=![]() 为定值.
为定值.
(I)由椭圆的离心率e=![]() =
=![]() =
=![]() ,则b2=
,则b2=![]() a2,
a2,
则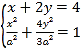 ,消去x,整理得:
,消去x,整理得:![]() y2﹣16y+16﹣a2=0,①
y2﹣16y+16﹣a2=0,①
由△=0,解得:a2=4,b2=3,
所以椭圆的标准方程为:![]() +
+![]() =1;所以
=1;所以![]() =
=![]() ,则T(1,
,则T(1,![]() ),
),
(Ⅱ)设直线l′的方程为y=![]() x+t,由
x+t,由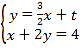 ,解得P的坐标为(1﹣
,解得P的坐标为(1﹣![]() ,
,![]() +
+![]() ),
),
所以|PT|2=![]() t2,
t2,
设设A(x1,y1),B(x2,y2),联立 ,消去y整理得x2+tx+
,消去y整理得x2+tx+![]() ﹣1=0,
﹣1=0,
则x1+x2=﹣t,x1x2=![]() ,△=t2﹣4(
,△=t2﹣4(![]() ﹣1)>0,t2<12,
﹣1)>0,t2<12,
y1=![]() x1+t,y2=
x1+t,y2=![]() x2+t,|PA|=
x2+t,|PA|=![]() =
=![]() |
|![]() ﹣x1|,
﹣x1|,
同理|PB|=![]() |
|![]() ﹣x2|,
﹣x2|,
|PA||PB|=![]() |(
|(![]() ﹣x1)(
﹣x1)(![]() ﹣x2)|=
﹣x2)|=![]() |
|![]() ﹣
﹣![]() (x1+x2)+x1x2|,
(x1+x2)+x1x2|,
![]() |
|![]() ﹣
﹣![]() (﹣t)+
(﹣t)+![]() |=
|=![]() t2,所以
t2,所以![]() =
=![]() =
=![]() ,
,
所以![]() =
=![]() 为定值.
为定值.


科目:高中数学 来源: 题型:
【题目】2019年,泉州市区的房价依旧是市民关心的话题.总体来说,二手房房价有所下降;相比二手房而言,新房市场依然强劲,价格持续升高.已知销售人员主要靠售房提成领取工资.现统计泉州市某新房销售人员2019年一年的工资情况的结果如图所示,则下列说法正确的是( )
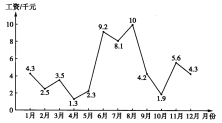
A.2019年该销售人员月工资的中位数为![]()
B.2019年该销售人员8月份的工资增长率最高
C.2019年该销售人员第一季度月工资的方差小于第二季度月工资的方差
D.2019年该销售人员第一季度月工资的平均数大于第四季度月工资的平均数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,过点F,斜率为1的直线与抛物线C交于点A,B,且
的焦点为F,过点F,斜率为1的直线与抛物线C交于点A,B,且![]() .
.
(1)求抛物线C的方程;
(2)过点Q(1,1)作直线交抛物线C于不同于R(1,2)的两点D、E,若直线DR,ER分别交直线![]() 于M,N两点,求|MN|取最小值时直线DE的方程.
于M,N两点,求|MN|取最小值时直线DE的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下统计表和分布图取自《清华大学2019年毕业生就业质量报告》.
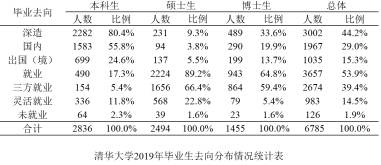
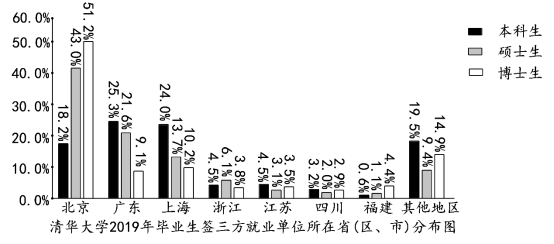
则下列选项错误的是( )
A.清华大学2019年毕业生中,大多数本科生选择继续深造,大多数硕士生选择就业
B.清华大学2019年毕业生中,硕士生的就业率比本科生高
C.清华大学2019年签三方就业的毕业生中,本科生的就业城市比硕士生的就业城市分散
D.清华大学2019年签三方就业的毕业生中,留北京人数超过一半
查看答案和解析>>
科目:高中数学 来源: 题型:
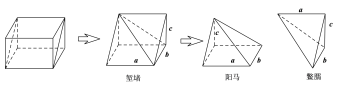
【题目】我国古代劳动人民在筑城、筑堤、挖沟、挖渠、建仓、建囤等工程中,积累了丰富的经验,总结出了一套有关体积、容积计算的方法,这些方法以实际问题的形式被收入我国古代数学名著《九章算术》中.《九章算术![]() 商功》:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”下图解释了这段话中由一个长方体,得到“堑堵”、“阳马”、“鳖臑”的过程.已知如图堑堵的棱长
商功》:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”下图解释了这段话中由一个长方体,得到“堑堵”、“阳马”、“鳖臑”的过程.已知如图堑堵的棱长![]() ,则鳖臑的外接球的体积为_________.
,则鳖臑的外接球的体积为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com