
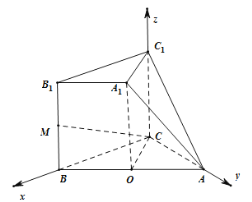
【题目】如图,在多面体![]() 中,正方形
中,正方形![]() 所在平面垂直于平面
所在平面垂直于平面![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,
,![]() .
.
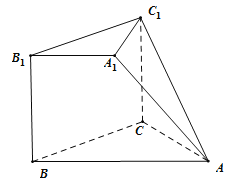
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)取![]() 中点
中点![]() ,连结
,连结![]() ,可证出四边形
,可证出四边形![]() 为平行四边形,利用等腰三角形和面面垂直的性质得出
为平行四边形,利用等腰三角形和面面垂直的性质得出![]() 和
和![]() ,最后根据线面垂直的判定定理,即可证出
,最后根据线面垂直的判定定理,即可证出![]() 平面
平面![]() ;
;
(2)由题可知,![]() 两两垂直,故以
两两垂直,故以![]() 为坐标原点建立空间直角坐标系,求出
为坐标原点建立空间直角坐标系,求出![]() 和平面
和平面![]() 的法向量,利用空间向量法求线面的夹角,即可得出直线
的法向量,利用空间向量法求线面的夹角,即可得出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
解:(1)可取![]() 中点
中点![]() ,连结
,连结![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形,
则![]() ,
,
由于![]() 是等腰直角三角形,
是等腰直角三角形,
则![]() ,
,
而正方形![]() 所在平面垂直于平面
所在平面垂直于平面![]() ,且
,且![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,即
,即![]() ,而
,而![]() ,
,
![]() 平面
平面![]() ,而
,而![]() ,
,
![]() 平面
平面![]() .
.
(2)易知![]() 两两垂直,故以
两两垂直,故以![]() 为坐标原点,
为坐标原点,
分别以![]() 的方向为
的方向为![]() 轴正方向建立空间直角坐标系,
轴正方向建立空间直角坐标系,
则各点坐标如下:![]() ,
,
![]() ,
,
则![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则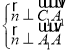 ,即
,即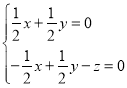 ,
,
令![]() ,则
,则![]() ,
,
![]() 平面
平面![]() 的法向量为
的法向量为![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则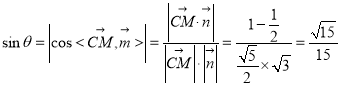 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某工厂生产某种电子产品,每件产品合格的概率均为![]() ,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验
,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验![]() 件该产品,且每件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检验方案:将产品每
件该产品,且每件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检验方案:将产品每![]() 个(
个(![]() )一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或
)一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或![]() 次.设该工厂生产
次.设该工厂生产![]() 件该产品,记每件产品的平均检验次数为
件该产品,记每件产品的平均检验次数为![]() .
.
(1)![]() 的分布列及其期望;
的分布列及其期望;
(2)(i)试说明,当![]() 越大时,该方案越合理,即所需平均检验次数越少;
越大时,该方案越合理,即所需平均检验次数越少;
(ii)当![]() 时,求使该方案最合理时
时,求使该方案最合理时![]() 的值及
的值及![]() 件该产品的平均检验次数.
件该产品的平均检验次数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正态分布有极其广泛的实际背景,生产与科学实验中很多随机变量的概率分布都可以近似地用正态分布来描述.例如,同一种生物体的身长、体重等指标.随着“绿水青山就是金山银山”的观念不断的深入人心,环保工作快速推进,很多地方的环境出现了可喜的变化.为了调查某水库的环境保护情况,在水库中随机捕捞了100条鱼称重.经整理分析后发现,鱼的重量x(单位:kg)近似服从正态分布![]() ,如图所示,已知
,如图所示,已知![]() .
.
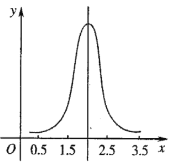
(Ⅰ)若从水库中随机捕捞一条鱼,求鱼的重量在![]() 内的概率;
内的概率;
(Ⅱ)(ⅰ)从捕捞的100条鱼中随机挑出6条鱼测量体重,6条鱼的重量情况如表.
重量范围(单位:kg) |
|
|
|
条数 | 1 | 3 | 2 |
为了进一步了解鱼的生理指标情况,从6条鱼中随机选出3条,记随机选出的3条鱼中体重在![]() 内的条数为X,求随机变量X的分布列和数学期望;
内的条数为X,求随机变量X的分布列和数学期望;
(ⅱ)若将选剩下的94条鱼称重做标记后立即放生.两周后又随机捕捞1000条鱼,发现其中带有标记的有2条.为了调整生态结构,促进种群的优化,预备捕捞体重在![]() 内的鱼的总数的40%进行出售,试估算水库中鱼的条数以及应捕捞体重在
内的鱼的总数的40%进行出售,试估算水库中鱼的条数以及应捕捞体重在![]() 内的鱼的条数.
内的鱼的条数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 为平面直角坐标系
为平面直角坐标系![]() 中的一个动点(其中
中的一个动点(其中![]() 为坐标系原点),点
为坐标系原点),点![]() 到定点
到定点![]() 的距离比到直线
的距离比到直线![]() 的距离大1,动点
的距离大1,动点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
①若![]() ,求直线
,求直线![]() 的直线方程;
的直线方程;
②分别过点![]() ,
,![]() 作曲线
作曲线![]() 的切线且交于点
的切线且交于点![]() ,是否存在以
,是否存在以![]() 为圆心,以
为圆心,以![]() 为半径的圆与经过点
为半径的圆与经过点![]() 且垂直于直线
且垂直于直线![]() 的直线
的直线![]() 相交于
相交于![]() 、
、![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
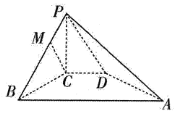
【题目】四棱锥![]() 中,PC⊥面ABCD,直角梯形ABCD中,∠B=∠C=90°,AB=4,CD=1,PC=2,点M在PB上且PB=4PM,PB与平面PCD所成角为60°.
中,PC⊥面ABCD,直角梯形ABCD中,∠B=∠C=90°,AB=4,CD=1,PC=2,点M在PB上且PB=4PM,PB与平面PCD所成角为60°.
(1)求证:![]() 面
面![]() :
:
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场的空调在1月到5月的销售量与月份相关,得到的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)经分析发现1月到5月的销售量可用线性回归模型拟合该商场空调的月销量![]() (百件)与月份
(百件)与月份![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测6月份该商场空调的销售量;
,并预测6月份该商场空调的销售量;
(2)若该商场的营销部对空调进行新一轮促销,对7月到12月有购买空调意愿的顾客进行问卷调查.假设该地拟购买空调的消费群体十分庞大,经过营销部调研机构对其中的500名顾客进行了一个抽样调查,得到如下一份频数表:
有购买意愿对应的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
频数 | 60 | 80 | 120 | 130 | 80 | 30 |
现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名,再从这6人中随机抽取3人进行跟踪调查,求抽出的3人中恰好有2人是购买意愿的月份是12月的概率.
参考公式与数据:线性回归方程![]() ,其中
,其中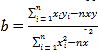 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,直线l:x+2y=4与椭圆有且只有一个交点T.
,直线l:x+2y=4与椭圆有且只有一个交点T.
(I)求椭圆C的方程和点T的坐标;
(Ⅱ)O为坐标原点,与OT平行的直线l′与椭圆C交于不同的两点A,B,直线l′与直线l交于点P,试判断![]() 是否为定值,若是请求出定值,若不是请说明理由.
是否为定值,若是请求出定值,若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:

则下面结论中不正确的是
A. 新农村建设后,种植收入减少
B. 新农村建设后,其他收入增加了一倍以上
C. 新农村建设后,养殖收入增加了一倍
D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了更好地贯彻党的“五育并举”的教育方针,某市要对全市中小学生“体能达标”情况进行了解,决定通过随机抽样选择几个样本校对学生进行体能达标测试,并规定测试成绩低于60分为不合格,否则为合格,若样本校学生不合格人数不超过其总人数的5%,则该样本校体能达标为合格.已知某样本校共有1000名学生,现从中随机抽取40名学生参加体能达标测试,首先将这40名学生随机分为甲、乙两组,其中甲乙两组学生人数的比为3:2,测试后,两组各自的成绩统计如下:甲组的平均成绩为70,方差为16,乙组的平均成绩为80,方差为36.
(1)估计该样本校学生体能测试的平均成绩;
(2)求该样本校40名学生测试成绩的标准差s;
(3)假设该样本校体能达标测试成绩服从正态分布![]() ,用样本平均数
,用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差s作为
,用样本标准差s作为![]() 的估计值
的估计值![]() ,利用估计值估计该样本校学生体能达标测试是否合格?
,利用估计值估计该样本校学生体能达标测试是否合格?
(注:1.本题所有数据的最后结果都精确到整数;2若随机变量z服从正态分布,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com