
【题目】某工厂生产某种电子产品,每件产品合格的概率均为![]() ,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验
,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验![]() 件该产品,且每件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检验方案:将产品每
件该产品,且每件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检验方案:将产品每![]() 个(
个(![]() )一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或
)一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或![]() 次.设该工厂生产
次.设该工厂生产![]() 件该产品,记每件产品的平均检验次数为
件该产品,记每件产品的平均检验次数为![]() .
.
(1)![]() 的分布列及其期望;
的分布列及其期望;
(2)(i)试说明,当![]() 越大时,该方案越合理,即所需平均检验次数越少;
越大时,该方案越合理,即所需平均检验次数越少;
(ii)当![]() 时,求使该方案最合理时
时,求使该方案最合理时![]() 的值及
的值及![]() 件该产品的平均检验次数.
件该产品的平均检验次数.
【答案】(1)分布列详见解析,期望![]() ;(2)(i)详见解析;(ii)
;(2)(i)详见解析;(ii)![]() 时平均检验次数最少,约
时平均检验次数最少,约![]() 次.
次.
【解析】
(1)根据每![]() 个(
个(![]() )一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或
)一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或![]() 次,每件产品的平均检验次数
次,每件产品的平均检验次数![]() 的可能取值为
的可能取值为![]() ,
,![]() ,再利用独立事件和互斥事件求得概率列出分布列,再求期望
,再利用独立事件和互斥事件求得概率列出分布列,再求期望
(2)(i)由(1)知![]() ,根据指数函数的单调性得到
,根据指数函数的单调性得到![]() 在
在![]() 上单调递减,从而得到结论. (ii)由(1)记
上单调递减,从而得到结论. (ii)由(1)记![]() ,则由
,则由![]() 且取最小值时,该方案最合理求解.
且取最小值时,该方案最合理求解.
(1)由题意,![]() 的可能取值为
的可能取值为![]() ,
,![]()
![]() ,
,![]() ,
,
故![]() 的分布列为
的分布列为
|
|
|
|
|
|
![]()
(2)(i)由(1),记![]() ,
,
因为![]() .所以
.所以![]() 在
在![]() 上单调递减,
上单调递减,
故![]() 越大,
越大,![]() 越小,即所需平均检验次数越少,该方案越合理.
越小,即所需平均检验次数越少,该方案越合理.
(ii)记![]() ,当
,当![]() 且取最小值时,该方案最合理,
且取最小值时,该方案最合理,
因为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() 时平均检验次数最少,约
时平均检验次数最少,约![]() 次.
次.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
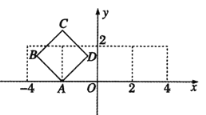
【题目】在平面直角坐标系![]() 中,如图放置的边长为2的正方形ABCD沿
中,如图放置的边长为2的正方形ABCD沿![]() 轴滚动(无滑动滚动),点D恰好经过坐标原点,设顶点
轴滚动(无滑动滚动),点D恰好经过坐标原点,设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则对函数
,则对函数![]() 的判断正确的是( )
的判断正确的是( )
A.函数![]() 在
在![]() 上有两个零点
上有两个零点
B.函数![]() 是偶函数
是偶函数
C.函数![]() 在
在![]() 上单调递增
上单调递增
D.对任意的![]() ,都有
,都有![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥![]() 中,顶点
中,顶点![]() 在底面
在底面![]() 的投影为
的投影为![]() 的内心,三个侧面的面积分别为12,16,20,且底面面积为24,则三棱锥
的内心,三个侧面的面积分别为12,16,20,且底面面积为24,则三棱锥![]() 的内切球的表面积为( )
的内切球的表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
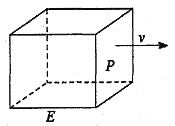
【题目】如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为![]() ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为![]() 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与![]() ×S成正比,比例系数为
×S成正比,比例系数为![]() ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为![]() ,记
,记![]() 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=![]() 时。
时。
(1)写出![]() 的表达式
的表达式
(2)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度![]() ,使总淋雨量
,使总淋雨量![]() 最少。
最少。
查看答案和解析>>
科目:高中数学 来源: 题型:
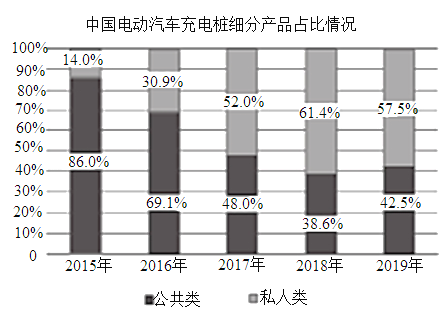
【题目】下图统计了截止到2019年年底中国电动汽车充电桩细分产品占比及保有量情况,关于这5次统计,下列说法正确的是( )
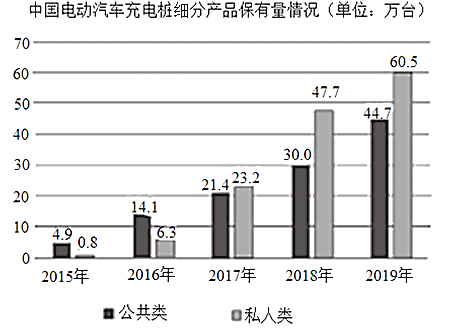
A.私人类电动汽车充电桩保有量增长率最高的年份是2018年
B.公共类电动汽车充电桩保有量的中位数是25.7万台
C.公共类电动汽车充电桩保有量的平均数为23.12万台
D.从2017年开始,我国私人类电动汽车充电桩占比均超过50%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,泉州市区的房价依旧是市民关心的话题.总体来说,二手房房价有所下降;相比二手房而言,新房市场依然强劲,价格持续升高.已知销售人员主要靠售房提成领取工资.现统计泉州市某新房销售人员2019年一年的工资情况的结果如图所示,则下列说法正确的是( )
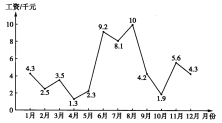
A.2019年该销售人员月工资的中位数为![]()
B.2019年该销售人员8月份的工资增长率最高
C.2019年该销售人员第一季度月工资的方差小于第二季度月工资的方差
D.2019年该销售人员第一季度月工资的平均数大于第四季度月工资的平均数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为原点,抛物线![]() 的准线与y轴的交点为H,P为抛物线C上横坐标为4的点,已知点P到准线的距离为5.
的准线与y轴的交点为H,P为抛物线C上横坐标为4的点,已知点P到准线的距离为5.
(1)求C的方程;
(2)过C的焦点F作直线l与抛物线C交于A,B两点,若以AH为直径的圆过B,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com