
【题目】四棱锥![]() 中,PC⊥面ABCD,直角梯形ABCD中,∠B=∠C=90°,AB=4,CD=1,PC=2,点M在PB上且PB=4PM,PB与平面PCD所成角为60°.
中,PC⊥面ABCD,直角梯形ABCD中,∠B=∠C=90°,AB=4,CD=1,PC=2,点M在PB上且PB=4PM,PB与平面PCD所成角为60°.
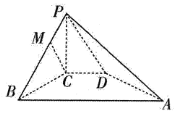
(1)求证:![]() 面
面![]() :
:
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析.(2)![]()
【解析】
(1)在线段AB上取一点N,使![]() ,可证
,可证![]() 平面
平面![]() ,由
,由![]() ,可得
,可得![]() ,得到
,得到![]() 平面
平面![]() ,从而可证面面平行,再根据面面平行得结果;
,从而可证面面平行,再根据面面平行得结果;
(2)以C为原点,CB,CD,CP所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间坐标系,用向量法求解二面角.
轴,建立空间坐标系,用向量法求解二面角.
(1)在线段AB上取一点N,使![]() ,
,
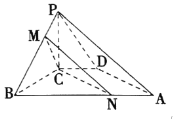
因为![]() ,所以
,所以![]() 且
且![]() ,
,
所以![]() 为平行四边形,
为平行四边形,
所以![]() ,
, ![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,则
,则![]() 平面
平面![]()
在三角形ABP中,![]() ,所以
,所以![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,则
,则![]() 平面
平面![]()
![]() 所以平面MNC//平面PAD,又
所以平面MNC//平面PAD,又![]() 平面MNC,
平面MNC,
所以CM![]() 平面PAD
平面PAD
(2)以C为原点,CB,CD,CP所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间坐标系.
轴,建立空间坐标系.
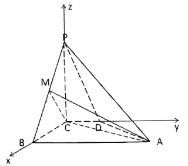
![]() 面ABCD,所以
面ABCD,所以![]() ,
,
又因为![]() ,所以
,所以![]() 面
面![]() ,
,
所以![]() 在面PCD的射影为PC,
在面PCD的射影为PC,
所以![]() 与平面PCD所成角,
与平面PCD所成角,
所以![]()
所以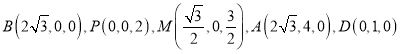 ,
,
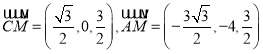 .
.
面![]() 法向量
法向量![]() ,
,
面![]() 法向量
法向量![]()
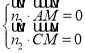 ,所以
,所以![]() ,
,
所以![]() ,
,
所以二面角![]() 所成角的余弦值为
所成角的余弦值为![]()


科目:高中数学 来源: 题型:
【题目】如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为![]() ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为![]() 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与![]() ×S成正比,比例系数为
×S成正比,比例系数为![]() ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为![]() ,记
,记![]() 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=![]() 时。
时。
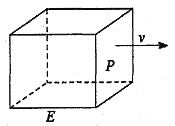
(1)写出![]() 的表达式
的表达式
(2)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度![]() ,使总淋雨量
,使总淋雨量![]() 最少。
最少。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,且
,且![]() .过椭圆的右焦点
.过椭圆的右焦点![]() 作长轴的垂线与椭圆,在第一象限交于点
作长轴的垂线与椭圆,在第一象限交于点![]() ,且满足
,且满足![]() .
.
(1)求椭圆的标准方程;
(2)若矩形![]() 的四条边均与椭圆相切,求该矩形面积的取值范围.
的四条边均与椭圆相切,求该矩形面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】CPI是居民消费价格指数的简称,是一个反映居民家庭一般所购买的消费品和服务项目价格水平变动情况的宏观经济指标.同比一般情况下是今年第n月与去年第n月比;环比,表示连续2个统计周期(比如连续两月)内的量的变化比.如图是根据国家统计局发布的2019年4月—2020年4月我国CPI涨跌幅数据绘制的折线图,根据该折线图,则下列说法正确的是( )
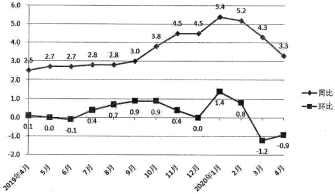
A.2020年1月CPI同比涨幅最大
B.2019年4月与同年12月相比较,4月CPI环比更大
C.2019年7月至12月,CPI一直增长
D.2020年1月至4月CPI只跌不涨
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小赵和小王约定在早上![]() 至
至![]() 之间到某公交站搭乘公交车去上学,已知在这段时间内,共有
之间到某公交站搭乘公交车去上学,已知在这段时间内,共有![]() 班公交车到达该站,到站的时间分别为
班公交车到达该站,到站的时间分别为![]() ,
,![]() ,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com