
【题目】[选修4-5:不等式选讲]
已知函数![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的解集;
的解集;
(Ⅱ)当![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
【解析】试题分析:(Ⅰ)利用零点分段去绝对值求解即可;
(Ⅱ)当![]() 时,
时, ![]() 恒成立,即
恒成立,即![]() ,显然当
,显然当![]() 时,不等式恒成立,当
时,不等式恒成立,当![]() 时,讨论
时,讨论![]() 和定义域的关系即可.
和定义域的关系即可.
试题解析:
(Ⅰ)当![]() 时,由
时,由![]() ,可得
,可得![]() ,
,
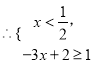 ①或
①或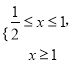 ②或
②或![]() ③
③
解①求得![]() ,解②求得
,解②求得![]() ,解③求得
,解③求得![]() ,
,
综上可得不等式的解集为![]() .
.
(Ⅱ)∵当![]() 时,
时, ![]() 恒成立,即
恒成立,即![]() ,
,
当![]() 时,
时, ![]() ;
;
当![]() 时,
时,
若![]() ,即
,即![]() 时,
时, ![]() ,
, ![]() ,所以
,所以![]() ;
;
若![]() ,即
,即![]() 时,
时, ![]() ,
, ![]() ,所以
,所以![]() ;
;
若![]() ,即
,即![]() 时,
时, ![]() 时,不等式不成立
时,不等式不成立
综上, ![]() .
.
点晴:含绝对值不等式的解法有两个基本方法,一是运用零点分区间讨论,二是利用绝对值的几何意义求解.第二问将绝对值不等式与函数以及不等式恒成立交汇、渗透,解题时强化函数、数形结合与转化化归思想方法的灵活应用,这是命题的新动向.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在正四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,下列四个结论不成立的是 ( )
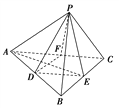
A. BC∥平面PDF B. DF⊥平面PAE
C. 平面PDF⊥平面PAE D. 平面PDE⊥平面ABC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的中心在原点,焦点为![]() ,
,![]() 且离心率
且离心率![]() .
.
(1)求双曲线的方程;
(2)求以点![]() 为中点的弦所在的直线方程.
为中点的弦所在的直线方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据焦点坐标求得![]() ,根据离心率及
,根据离心率及![]() 求得
求得![]() 的值,进而求得双曲线的标准方程.(2)设出
的值,进而求得双曲线的标准方程.(2)设出![]() 两点的坐标,利用点差法求得弦所在直线的斜率,再由点斜式求得弦所在的直线方程.
两点的坐标,利用点差法求得弦所在直线的斜率,再由点斜式求得弦所在的直线方程.
(1) 由题可得![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
所以双曲线方程 ![]() .
.
(2)设弦的两端点分别为![]() ,
,![]() ,
,
则由点差法有: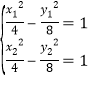 , 上下式相减有:
, 上下式相减有:![]()
又因为![]() 为中点,所以
为中点,所以![]() ,
,![]() ,
,
∴![]() ,所以由直线的点斜式可得
,所以由直线的点斜式可得![]() ,
,
即直线的方程为![]() .
.
经检验满足题意.
【点睛】
本小题主要考查双曲线标准方程的求法,考查利用点差法求解有关弦的中点有关的问题,属于中档题
【题型】解答题
【结束】
19
【题目】某投资公司计划投资![]() ,
,![]() 两种金融产品,根据市场调查与预测,
两种金融产品,根据市场调查与预测,![]() 产品的利润
产品的利润![]() 与投资金额
与投资金额![]() 的函数关系为
的函数关系为![]() ,
,![]() 产品的利润
产品的利润![]() 与投资金额
与投资金额![]() 的函数关系为
的函数关系为![]() .(注:利润与投资金额单位:万元)
.(注:利润与投资金额单位:万元)
(1)该公司已有100万元资金,并全部投入![]() ,
,![]() 两种产品中,其中
两种产品中,其中![]() 万元资金投入
万元资金投入![]() 产品,试把
产品,试把![]() ,
,![]() 两种产品利润总和表示为
两种产品利润总和表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)试问:怎样分配这100万元资金,才能使公司获得最大利润?其最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内动点![]() 到两定点
到两定点![]() 和
和![]() 的距离之和为4.
的距离之和为4.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)已知直线![]() 和
和![]() 的倾斜角均为
的倾斜角均为![]() ,直线
,直线![]() 过坐标原点
过坐标原点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,直线
两点,直线![]() 过点
过点![]() 且与曲线
且与曲线![]() 是交于
是交于![]() ,
, ![]() 两点,求证:对任意
两点,求证:对任意![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只小蜜蜂位于数轴上的原点处,小蜜蜂每一次具有只向左或只向右飞行一个单位或者两个单位距离的能力,且每次飞行至少一个单位.若小蜜蜂经过5次飞行后,停在数轴上实数3位于的点处,则小蜜蜂不同的飞行方式有多少种?( )
A. 5 B. 25 C. 55 D. 75
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最大值为
的最大值为![]() ,
, ![]() 的图像关于
的图像关于![]() 轴对称.
轴对称.
(1)求实数![]() ,
, ![]() 的值.
的值.
(2)设![]() ,则是否存在区间
,则是否存在区间![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ?若存在,求实数
?若存在,求实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以![]() 表示值域为
表示值域为![]() 的函数组成的集合,
的函数组成的集合,![]() 表示具有如下性质的函数
表示具有如下性质的函数![]() 组成的集合:对于函数
组成的集合:对于函数![]() ,存在一个正数
,存在一个正数![]() ,使得函数
,使得函数![]() 的值域包含于区间
的值域包含于区间![]() 。例如,当
。例如,当![]() ,
,![]() 时,
时,![]() ,
,![]() 。则下列命题中正确的是:( )
。则下列命题中正确的是:( )
A.设函数![]() 的定义域为
的定义域为![]() ,则“
,则“![]() ”的充要条件是“
”的充要条件是“![]() ,
,![]() ,
,![]() ”
”
B.函数![]() 的充要条件是
的充要条件是![]() 有最大值和最小值
有最大值和最小值
C.若函数![]() ,
,![]() 的定义域相同,且
的定义域相同,且![]() ,
,![]() ,则
,则![]()
D.若函数![]() 有最大值,则
有最大值,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() 的参数方程是
的参数方程是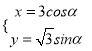 (
(![]() 为参数)以原点为极点,
为参数)以原点为极点, ![]() 轴正半轴为极轴,并取与直角坐标系相同的单位长度,建立极坐标系,曲线
轴正半轴为极轴,并取与直角坐标系相同的单位长度,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求曲线![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 、
、![]() 分别是曲线
分别是曲线![]() 和
和![]() 上的任意点,求
上的任意点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com