
【题目】已知函数![]() 的最大值为
的最大值为![]() ,
, ![]() 的图像关于
的图像关于![]() 轴对称.
轴对称.
(1)求实数![]() ,
, ![]() 的值.
的值.
(2)设![]() ,则是否存在区间
,则是否存在区间![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ?若存在,求实数
?若存在,求实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)![]() ,
, ![]() .(2)见解析.
.(2)见解析.
【解析】【试题分析】(1)对![]() 求导,利用它的单调性求得当
求导,利用它的单调性求得当![]() 时函数取得最大值,解方程求得
时函数取得最大值,解方程求得![]() .根据二次函数的对称轴可求得
.根据二次函数的对称轴可求得![]() .(2)由(1)知
.(2)由(1)知![]() ,利用
,利用![]() 的二阶导数判断出函数
的二阶导数判断出函数![]() 在区间
在区间![]() 内单调递增,故有
内单调递增,故有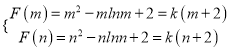 , 问题转化为关于
, 问题转化为关于![]() 的方程
的方程![]() 在区间
在区间![]() 内是否存在两个不相等的实根来求解.利用分离常数法将
内是否存在两个不相等的实根来求解.利用分离常数法将![]() 分离出来后利用导数证明
分离出来后利用导数证明![]() 不存在.
不存在.
【试题解析】
(1)由题意得![]() ,令
,令![]() ,解得
,解得![]() ,
,
当![]() 时,
时, ![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,函数
,函数![]() 单调递减.
单调递减.
所以当![]() 时,
时, ![]() 取得极大值,也是最大值,所以
取得极大值,也是最大值,所以![]() ,解得
,解得![]() .
.
又![]() 的图像关于
的图像关于![]() 轴对称,所以
轴对称,所以![]() ,解得
,解得![]() .
.
(2)由(1)知![]() ,
, ![]() ,则
,则![]() ,所以
,所以![]() ,令
,令![]() ,则
,则![]() 对
对![]() 恒成立,
恒成立,
所以![]() 在区间
在区间![]() 内单调递增,所以
内单调递增,所以![]() 恒成立,
恒成立,
所以函数![]() 在区间
在区间![]() 内单调递增.
内单调递增.
假设存在区间![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上的值域是
上的值域是![]() ,
,
则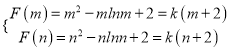 ,
,
问题转化为关于![]() 的方程
的方程![]() 在区间
在区间![]() 内是否存在两个不相等的实根,
内是否存在两个不相等的实根,
即方程![]() 在区间
在区间![]() 内是否存在两个不相等的实根,
内是否存在两个不相等的实根,
令![]() ,
, ![]() ,则
,则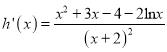 ,
,
设![]() ,
, ![]() ,则
,则![]() 对
对![]() 恒成立,所以函数
恒成立,所以函数![]() 在区间
在区间![]() 内单调递增,故
内单调递增,故![]() 恒成立,所以
恒成立,所以![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 内单调递增,所以方程
内单调递增,所以方程![]() 在区间
在区间![]() 内不存在两个不相等的实根.
内不存在两个不相等的实根.
综上所述,不存在区间![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上的值域是
上的值域是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设H1(x)=max![]() ,H2(x)=min
,H2(x)=min![]() (max
(max![]() 表示p,q中的较大值,min
表示p,q中的较大值,min![]() 表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
A.16B.-16
C.a2-2a-16D.a2+2a-16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为![]() 、
、![]() 、
、![]() 三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).


(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以直角坐标系的原点
为参数),在以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某市主办的科技知识竞赛的学生成绩中随机选取了40名学生的成绩作为样本,已知这些成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组![]() ;第二组
;第二组![]() ;
;![]() ;第六组
;第六组![]() ,并据此绘制了如图所示的频率分布直方图.
,并据此绘制了如图所示的频率分布直方图.
![]() 求成绩在区间
求成绩在区间![]() 内的学生人数;
内的学生人数;
![]() 估计这40名学生成绩的众数和中位数.
估计这40名学生成绩的众数和中位数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,河的两岸分别有生活小区![]() 和
和![]() ,其中
,其中![]() ,
,![]() 三点共线,
三点共线,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,测得
,测得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,若以
,若以![]() 所在直线分别为
所在直线分别为![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() 则河岸
则河岸![]() 可看成是曲线
可看成是曲线![]() (其中
(其中![]() 是常数)的一部分,河岸
是常数)的一部分,河岸![]() 可看成是直线
可看成是直线![]() (其中
(其中![]() 为常数)的一部分.
为常数)的一部分.

(1)求![]() 的值.
的值.
(2)现准备建一座桥![]() ,其中
,其中![]() 分别在
分别在![]() 上,且
上,且![]() ,
,![]() 的横坐标为
的横坐标为![]() .写出桥
.写出桥![]() 的长
的长![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ,并标明定义域;当
,并标明定义域;当![]() 为何值时,
为何值时,![]() 取到最小值?最小值是多少?
取到最小值?最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={x|x<-3,或x>5},P={x|(x-a)·(x-8)≤0}.
(1)求M∩P={x|5<x≤8}的充要条件;
(2)求实数a的一个值,使它成为M∩P={x|5<x≤8}的一个充分但不必要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3-x2=2.
(1)求数列{xn}的通项公式;
(2)如图,在平面直角坐标系xOy中,依次连接点P1(x1,1),P(x2,2),…,Pn+1(xn+1,n+1)得到折线P1P2…Pn+1,求由该折线与直线y=0,x=x1,x=xn+1所围成的区域的面积Tn.
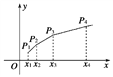
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com