
| A. | 125天 | B. | 100天 | C. | 50天 | D. | 75天 |
分析 由题意得V=a•e-50k=$\frac{4}{9}$a,可令t天后体积变为$\frac{8}{27}$a,即有V=a•e-kt=$\frac{8}{27}$a,由此能求出结果.
解答 解:由题意得V=a•e-50k=$\frac{4}{9}$a,①
可令t天后体积变为$\frac{8}{27}$a,即有V=a•e-kt=$\frac{8}{27}$a,②
由①可得e-50k=$\frac{4}{9}$,③
又②÷①得e-(t-50)k=$\frac{2}{3}$,
两边平方得e-(2t-100)k=$\frac{4}{9}$,
与③比较可得2t-100=50,解得t=75,
即经过75天后,体积变为$\frac{8}{27}$a.
故选:D.
点评 本题考查函数有生产生活中的应用,是中档题,解题时要认真审题,注意挖掘题设中的隐含条件,合理建立方程.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
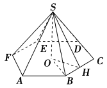 正六棱锥得底面周长为24,O是底面的中心,H是BC的中点,∠SHO=60°.
正六棱锥得底面周长为24,O是底面的中心,H是BC的中点,∠SHO=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 7 | 4 | 5 | 8 | 1 | 3 | 5 | 2 | 6 |
| A. | 9400 | B. | 9408 | C. | 9410 | D. | 9414 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | -1 | 0 | 1 | 2 | 3 |
| f(x) | -0.677 | 3.011 | 5.432 | 5.980 | 7.651 |
| g(x) | -0.530 | 3.451 | 4.890 | 5.241 | 6.892 |
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -4 | C. | -5 | D. | $-\frac{15}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com