
【题目】培养某种水生植物需要定期向培养植物的水中加入物质![]() ,已知向水中每投放1个单位的物质
,已知向水中每投放1个单位的物质![]() ,
,![]() (单位:天)时刻后水中含有物质
(单位:天)时刻后水中含有物质![]() 的量增加
的量增加![]() ,
,![]() 与
与![]() 的函数关系可近似地表示为关系可近似地表示为
的函数关系可近似地表示为关系可近似地表示为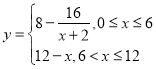 .根据经验,当水中含有物质
.根据经验,当水中含有物质![]() 的量不低
的量不低![]() 时,物质
时,物质![]() 才能有效发挥作用.
才能有效发挥作用.
(1)若在水中首次投放1个单位的物质![]() ,计算物质
,计算物质![]() 能持续有效发挥作用几天?
能持续有效发挥作用几天?
(2)若在水中首次投放1个单位的物质![]() ,第8天再投放1个单位的物质
,第8天再投放1个单位的物质![]() ,试判断第8天至第12天,水中所含物质
,试判断第8天至第12天,水中所含物质![]() 的量是否始终不超过
的量是否始终不超过![]() ,并说明理由.
,并说明理由.
【答案】(1)6天.(2)第8天至第12天,水中所含物质![]() 的量始终不超过
的量始终不超过![]() .见解析
.见解析
【解析】
(1)由题可知 ,分类讨论求解满足
,分类讨论求解满足![]() 时的
时的![]() 的范围,即可得出在水中首次投放1个单位的物质
的范围,即可得出在水中首次投放1个单位的物质![]() ,物质
,物质![]() 能持续有效发挥作用的天数;
能持续有效发挥作用的天数;
(2)根据已知求出函数解析式![]() ,利用基本不等式即可求得当
,利用基本不等式即可求得当![]() 时,
时,![]() ,从而得出结论.
,从而得出结论.
解:(1)由题意,![]() (单位:天)时刻后水中含有物质
(单位:天)时刻后水中含有物质![]() 的量为:
的量为:
 ,
,
由于当水中含有物质![]() 的量不低
的量不低![]() 时,物质
时,物质![]() 才能有效发挥作用,
才能有效发挥作用,
即需![]() ,
,
则当![]() 时,
时,![]() 且当
且当![]() 时,
时,![]() ,
,
解得:![]() ,
,
所以若在水中首次投放1个单位的物质![]() ,物质
,物质![]() 能持续有效发挥作用的时间为:8-2=6天.
能持续有效发挥作用的时间为:8-2=6天.
(2)设第![]() 天水中所含物质
天水中所含物质![]() 的量为
的量为![]() ,
,
则![]() ,
,
![]() ,
,
当且仅当![]() ,即
,即![]() 时,等号成立,
时,等号成立,
即当![]() 时,
时,![]() ,
,
所以第8天至第12天,水中所含物质![]() 的量始终不超过
的量始终不超过![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为准备参加市运动会,对本校甲、乙两个田径队中![]() 名跳高运动员进行了测试,并用茎叶图表示出本次测试
名跳高运动员进行了测试,并用茎叶图表示出本次测试![]() 人的跳高成绩(单位:
人的跳高成绩(单位:![]() ).跳高成绩在
).跳高成绩在![]() 以上(包括
以上(包括![]() )定义为“合格”,成绩在
)定义为“合格”,成绩在![]() 以下(不包括
以下(不包括![]() )定义为“不合格”.鉴于乙队组队晚,跳高成绩相对较弱,为激励乙队队队,学校决定只有乙队中“合格”者才能参加市运动会开幕式旗林队.
)定义为“不合格”.鉴于乙队组队晚,跳高成绩相对较弱,为激励乙队队队,学校决定只有乙队中“合格”者才能参加市运动会开幕式旗林队.
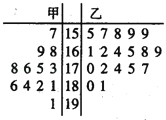
(1)求甲队队员跳高成绩的中位数;
(2)如果用分层抽样的方法从甲、乙两队所有的运动员中共抽取![]() 人,则
人,则![]() 人中“合格”与“不合格”的人数各为多少;
人中“合格”与“不合格”的人数各为多少;
(3)若从所有“合格”运动员中选取![]() 名,用
名,用![]() 表示所选运动员中能参加市运动会开幕式旗林队的人数,试求
表示所选运动员中能参加市运动会开幕式旗林队的人数,试求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆台![]() 的轴截面为等腰梯形
的轴截面为等腰梯形![]() ,
,![]() ,
,![]() ,
,![]() ,圆台
,圆台![]() 的侧面积为
的侧面积为![]() .若点C,D分别为圆
.若点C,D分别为圆![]() ,
,![]() 上的动点且点C,D在平面
上的动点且点C,D在平面![]() 的同侧.
的同侧.
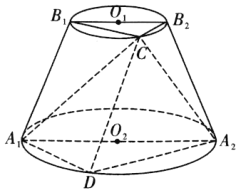
(1)求证:![]() ;
;
(2)若![]() ,则当三棱锥
,则当三棱锥![]() 的体积取最大值时,求多面体
的体积取最大值时,求多面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】蜂巢是由工蜂分泌蜂蜡建成的.从正面看,蜂巢口是由许多正六边形的中空柱状体连接而成,中空柱状体的底部是由三个全等的菱形面构成.如图,在正六棱柱![]() 的三个顶点
的三个顶点![]() 处分别用平面
处分别用平面![]() ,平面
,平面![]() ,平面
,平面![]() 截掉三个相等的三棱锥
截掉三个相等的三棱锥![]() ,
,![]() ,
,![]() ,平面
,平面![]() ,平面
,平面![]() ,平面
,平面![]() 交于点
交于点![]() ,就形成了蜂巢的结构,如下图(4)所示,
,就形成了蜂巢的结构,如下图(4)所示,
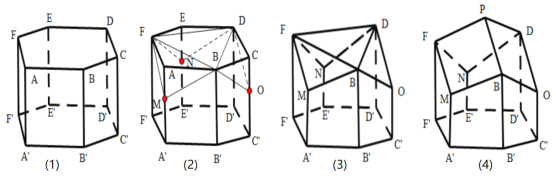
瑞士数学家克尼格利用微积分的方法证明了蜂巢的这种结构是在相同容积下所用材料最省的,英国数学家麦克劳林通过计算得到菱形的一个内角为![]() ,即
,即![]() .以下三个结论①
.以下三个结论①![]() ;②
;② ![]()
![]()
![]() ;③
;③![]() 四点共面,正确命题的个数为______个;若
四点共面,正确命题的个数为______个;若![]() ,
,![]() ,
,![]() ,则此蜂巢的表面积为_______.
,则此蜂巢的表面积为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com