练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    平面直角坐标系中，已知A（4，3），试在x轴上求一点P，使
    OP
    AP
    的值最大．
    考点：函数与方程的综合运用,函数的最值及其几何意义
    专题：函数的性质及应用
    分析：设出P的坐标，利用距离公式表示所求表达式，利用二次函数的最值求解最值即可．
    解答： 解：由题意设P（x，0）．如图，显然x＞0，
    OP
    AP
    的值大于x＜0时的值．
    OP
    AP
    =
    x2
    (x-4)2+32
    =
    x2
    x2-8x+25
    =
    1
    1-
    8
    x
    +
    25
    x2
    ，
    当1-
    8
    x
    +
    25
    x2
    取得最小值时
    OP
    AP
    取得最大值．
    当
    1
    x
    =
    8
    2×25
    =
    4
    25
    ，即x=
    25
    4
    时，1-
    8
    x
    +
    25
    x2
    取得最小值：
    9
    25
    ，
    OP
    AP
    的最大值为：
    1
    9
    25
    =
    5
    3
    ．
    此时P（
    25
    4
    ，0）．
    点评：本题考查函数与方程的综合应用，考查转化思想以及计算能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    定义：点M（a，b）的“相关函数”为f（x）=asinx+bcosx（x∈R），点M（a，b）称为函数f（x）=asinx+bcosx（x∈R）的“相关点”．
    （I）设函数h（x）=
    		2
    ×（
    1
    3
    ）mcos（x-
    π
    4
    ）-2sin（x+
    π
    6
    ）的“相关点”为N，若N∈{（a，b）|a＜0，b＞0，a∈R，b∈R}，求实数m的取值范围；
    （Ⅱ）已知点M（a，b）满足：
    b
    a
    ∈（1，
    		2
    ]，点M（a，b）的“相关函数”f（x）在x=x0处取得最大值，求tan2x0的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设f（x）=asin（πx+α）+bcos（πx+β），其中a、b、α、β为非零常数．若f（2013）=-1，则f（2014）等于（　　）
    A、-1B、0C、1D、2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知集合A={x|x2-3x-10＜0}，B={x|m+1≤x≤2m-1}．
    （1）当m=3时，求集合A∩B（∁RA）∩B；
    （2）若A∩B=B，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如果sin（α-
    π
    6
    ）=
    1
    3
    ，求sin（2α+
    π
    6
    ）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某公司试销 一种新产品，规定试销时销售单 价不低于成本单价500元/件，又不高于800元/件，经试销调查，发现销售量y（件）与销售单价x（元/件），可近似看做一次函数y=kx+b的关系（图象如图所示）． 
    （1）根据图象，求一次函数y=kx+b的表达式； 
    （2）设公司获得的毛利润（毛利润=销售 总价-成本总价）为S元，①求S关于x的函数表达式； ②求该公司可获得的最大毛利润，并求出 此时相应的销售单价．x=600y=600．x=700y=450．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

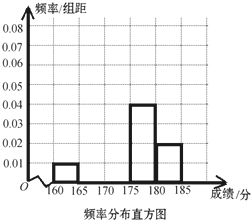    永安市教育局在2013年高职单招考试成绩中随机抽取100名学生的成绩，按成绩分组，得到频率分布表如下所示：
    组号分组频数频率
    第1组[160，165）50.050
    第2组[165，170）①
     
    		0.350
    第3组[170，175）30②
     
    第4组[175，180）200.200
    第5组[180，185）100.100
    合计1001.000
    （1）请先求出频率分布表中①②位置相应的数据（直接写在表中），再将如图频率分布直方图补充完整；
    （2）教育局决定在成绩高的第3，4，5组中用分层抽样抽取6名学生进行奖励，则第3，4，5组每组各抽取多少名学生？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知平行六面体ABCD-A′B′C′D′中，AB=4，AD=3，AA′=5，∠BAD=∠BAA′=∠DAA′=60°，则AC′的长为（　　）
    A、5
    		2
    B、
    		62
    C、10
    D、
    		97

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设双曲线
    x2
    a2
    -
    y2
    b2
    =1（a＞0，b＞0）的离心率为
    		3
    ，且它的一个焦点与抛物线y2=24x的焦点重合，则此双曲线的方程为（　　）
    A、
    x2
    12
    -
    y2
    24
    =1
    B、
    x2
    48
    -
    y2
    96
    =1
    C、
    x2
    3
    -
    2y2
    3
    =1
    D、
    x2
    3
    -
    y2
    6
    =1

    查看答案和解析>>

    同步练习册答案