【思路点拨】求出导函数,根据导函数有零点,求a的取值范围.
解:由题意知该函数的定义域为(0,+∞),且f'(x)=2ax+

.因为存在垂直于y轴的切线,故此时斜率为0,问题转化为x>0时导函数f'(x)=2ax+

存在零点的问题.
方法一(图象法):将之转化为g(x)=-2ax与h(x)=

存在交点.
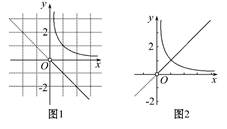
当a=0时不符合题意,当a>0时,如图1,数形结合可得没有交点,当a<0时,如图2,此时正好有一个交点,故有a<0,应填(-∞,0).
方法二(分离变量法):可等价于方程2ax+

=0在(0,+∞)内有解,显然可得a=-
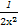
∈(-∞,0).
