
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1(y≠0) | B. | $\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{5}$=1(x≠0) | C. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1(x≠3) | D. | $\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{5}$=1(y≠3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在三棱锥D-ABC,AB=BC=CD=DA=8,∠ADC=∠ABC=120°,M、O分别为棱BC,AC的中点,DM=4$\sqrt{2}$.
在三棱锥D-ABC,AB=BC=CD=DA=8,∠ADC=∠ABC=120°,M、O分别为棱BC,AC的中点,DM=4$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
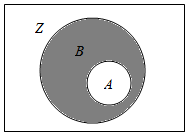 已知集合A={x∈Z|$\frac{x+1}{2-x}$≥0),B={x∈Z|-2<x≤3),则图中阴影部分表示的集合是( )
已知集合A={x∈Z|$\frac{x+1}{2-x}$≥0),B={x∈Z|-2<x≤3),则图中阴影部分表示的集合是( )| A. | {1,2,3) | B. | {2,3} | C. | {1,3} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
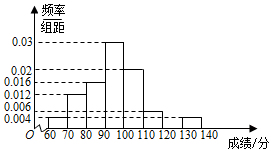 某校在一次期末考试中,全校学生的数学成绩都介于60分到140分之间(满分150分),为了估计该校学生的数学考试情况,从该校2000名学生的数学成绩中随机抽取50名学生的数学成绩,将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140].如图是按照上述分组得到的频率分布直方图的一部分.估计该校2000名学生这次考试的数学成绩的平均分为97.
某校在一次期末考试中,全校学生的数学成绩都介于60分到140分之间(满分150分),为了估计该校学生的数学考试情况,从该校2000名学生的数学成绩中随机抽取50名学生的数学成绩,将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140].如图是按照上述分组得到的频率分布直方图的一部分.估计该校2000名学生这次考试的数学成绩的平均分为97.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com