
【题目】在某大学自主招生考试中,所有选报Ⅱ类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五个等级.某考场考生两科的考试成绩的数据如下图所示,其中“数学与逻辑”科目的成绩为
五个等级.某考场考生两科的考试成绩的数据如下图所示,其中“数学与逻辑”科目的成绩为![]() 的考生有
的考生有![]() 人.
人.
(Ⅰ)求该考场考生中“阅读与表达”科目中成绩为![]() 的人数.
的人数.
(Ⅱ)若等级![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别对应
分别对应![]() 分,
分, ![]() 分,
分, ![]() 分,
分, ![]() 分,
分, ![]() 分.
分.
(ⅰ)求该考场考生“数学与逻辑”科目的平均分.
(ⅱ)若该考场共有![]() 人得分大于
人得分大于![]() 分,其中有
分,其中有![]() 人
人![]() 分,
分, ![]() 人
人![]() 分,
分, ![]() 人
人![]() 分.
分.
从这![]() 人中随机抽取两人,求两人成绩之和的分布列和数学期望.
人中随机抽取两人,求两人成绩之和的分布列和数学期望.
科目:数学与逻辑 | 科目:阅读与表达 |
|
|
【答案】(Ⅰ)3 (Ⅱ)ⅰ:平均分为2.9 ⅱ:分布列见解析,数学期望为![]()
【解析】试题分析:(Ⅰ)由数学与逻辑中成绩等级为B的考生有10人,频率为![]() ,可求考场中的人数,然后结合其频率可求;(Ⅱ)ⅰ:结合频率分布直方图可求该考场考生“数学与逻辑”科目的平均分;ⅱ:设两人成绩之和为ξ,则ξ的值可以为16,17,18,19,20,然后求出ξ去每个值对应的概率,即可求解出ξ的分布列及ξ的数学期望;
,可求考场中的人数,然后结合其频率可求;(Ⅱ)ⅰ:结合频率分布直方图可求该考场考生“数学与逻辑”科目的平均分;ⅱ:设两人成绩之和为ξ,则ξ的值可以为16,17,18,19,20,然后求出ξ去每个值对应的概率,即可求解出ξ的分布列及ξ的数学期望;
试题解析:
(Ⅰ)∵“数学与逻辑”科目中等级为![]() 的考生有
的考生有![]() 人,
人,
∴考场共有![]() 人,
人,
∴“阅读与表达”科目中成绩等级为![]() 的人数为
的人数为
![]() 人.
人.
(Ⅱ)ⅰ:平均分为![]() 分,
分,
ⅱ:设两个人成绩之和为![]() ,则
,则![]() 的值可以为
的值可以为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
∴![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
|
|
∴![]() ,
,
∴![]() 的数学期望为
的数学期望为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的焦距为2,离心率为
的焦距为2,离心率为![]() ,
,![]() 轴上一点
轴上一点![]() 的坐标为
的坐标为![]() .
.
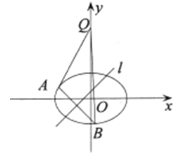
(Ⅰ)求该椭圆的方程;
(Ⅱ)若对于直线![]() ,椭圆
,椭圆![]() 上总存在不同的两点
上总存在不同的两点![]() 与
与![]() 关于直线
关于直线![]() 对称,且
对称,且![]() ,求
,求
实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1在平面直角坐标系中的参数方程为 (t为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,有曲线C2:ρ=2cosθ-4sinθ
(t为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,有曲线C2:ρ=2cosθ-4sinθ
(1)将C1的方程化为普通方程,并求出C2的平面直角坐标方程
(2)求曲线C1和C2两交点之间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=Asin(2x+ ![]() )(x∈R)的图象过点P(
)(x∈R)的图象过点P( ![]() ,﹣2). (Ⅰ)求f(x)的解析式;
,﹣2). (Ⅰ)求f(x)的解析式;
(Ⅱ)已知f( ![]() +
+ ![]() )=
)= ![]() ,﹣
,﹣ ![]() <a<0,求cos(a﹣
<a<0,求cos(a﹣ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ax2﹣(a﹣1)x﹣lnx(a∈R且a≠0).
ax2﹣(a﹣1)x﹣lnx(a∈R且a≠0).
(1)求函数f(x)的单调递增区间;
(2)记函数y=F(x)的图象为曲线C.设点A(x1 , y1),B(x2 , y2)是曲线C上的不同两点.如果在曲线C上存在点M(x0 , y0),使得:①x0= ![]() ;②曲线C在点M处的切线平行于直线AB,则称函数F(x)存在“中值和谐切线”.当a=2时,函数f(x)是否存在“中值和谐切线”,请说明理由.
;②曲线C在点M处的切线平行于直线AB,则称函数F(x)存在“中值和谐切线”.当a=2时,函数f(x)是否存在“中值和谐切线”,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知底角为45°的等腰梯形ABCD,底边BC长为12,腰长为4 ![]() ,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分.
,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分. 
(1)令BF=x(0<x<12),试写出直线右边部分的面积y与x的函数解析式;
(2)在(1)的条件下,令y=f(x).构造函数g(x)= ![]() .
.
①判断函数g(x)在(4,8)上的单调性;
②判断函数g(x)在定义域内是否具有单调性,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要付出设备的维修和工人工资等费用an的信息如图. 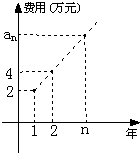
(1)求an;
(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com