[题目]设函数f(x)=Asin(2x+ )的图象过点P( .﹣2)．的解析式,(Ⅱ)已知f( + )= .﹣ ＜a＜0.求cos(a﹣ )的值．题目和参考答案——青夏教育精英家教网—

【题目】设函数f（x）=Asin（2x+ ）（x∈R）的图象过点P（，﹣2）．（Ⅰ）求f（x）的解析式；
（Ⅱ）已知f（ + ）= ，﹣ ＜a＜0，求cos（a﹣ ）的值．

【答案】解：（Ⅰ）∵f（x）的图象过点P（，﹣2）， ∴f（）=Asin（2× + ）=Asin =﹣2
∴A=2
故f（x）的解析式为f（x）=2sin（2x+ ）
（Ⅱ）∵f（ + ）=2cosα= ，∴cosα= ，
∵﹣ ＜a＜0，∴sinα=﹣ （9分）
∴cos（a﹣ ）=cosαcos +sinαsin =﹣
【解析】（Ⅰ）根据f（x）的图象过点P（，﹣2），可得f（）=Asin（2× + ）=Asin =﹣2，从而可求f（x）的解析式为；（Ⅱ）根据f（ + ）=2cosα= ，可得cosα= ，结合﹣ ＜a＜0，可得sinα=﹣ ，再利用差角的余弦公式，即可求得结论．

练习册系列答案

68所名校图书毕业升学全真模拟试卷系列答案

国华图书中考拐点系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知三棱柱ABC﹣A1B1C1的直观图和三视图如图所示，E是棱CC1上一点．
（1）若CE=2EC1 ，求三棱锥E﹣ACB1的体积．
（2）若E是CC1的中点，求C到平面AEB1的距离．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】函数f（x）的定义域为开区间（a，b），导函数f′（x）在（a，b）内的图象如图所示，则函数f（x）在开区间（a，b）内有极大值点（）
A.1个
B.2个
C.3个
D.4个

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在侧棱和底面垂直的三棱柱ABC﹣A1B1C1中，AB=1，AC= ，BC=2，AA1= ，点P为CC1的中点．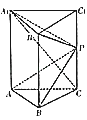
（1）求证：A1C⊥平面ABP；
（2）求平面ABP与平面A1B1P所成二面角的正弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】盒子中有大小相同的球6个，其中标号为1的球2个，标号为2的球3个．标号为3的球1个，第一次从盒子中任取1个球，放回后第二次再任取1个球（假设取到每个球的可能性都相同）．记第一次与第二次取到球的标号之和为ξ．
（1）求随机变量ξ的分布列：
（2）求随机变量ξ的期望Eξ．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为增强市民的节能环保意识，某市面向全市征召义务宣传志愿者．从符合条件的500名志愿者中随机抽取100名志愿者，其年龄频率分布直方图如图所示，其中年龄分组区间是：[20，25），[25，30），[30，35），[35，40），[40，45]．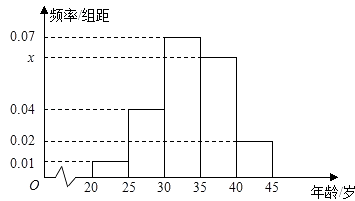

（Ⅰ）求图中x的值并根据频率分布直方图估计这500名志愿者中年龄在[35，40）岁的人数；
（Ⅱ）在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动，再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人．记这3名志愿者中“年龄低于35岁”的人数为X，求X的分布列及数学期望．