
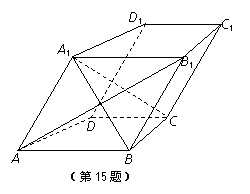
如图,在四棱柱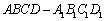 中,
中,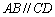 ,
,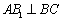 ,且
,且 .
.
(1)求 证:
证: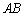 ∥平面
∥平面 ;
;
(2)求证: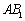 ⊥平面
⊥平面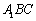 .
.
 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知等差数列{an}、等比数列{bn}满足a1+a2=a3,b1b2=b3,且a3,a2+ b1,a1+ b2成等差数列,a1,a2,b2成等比数列.
(1)求数列{an}和数列{bn}的通项公式;
(2)按如下方法从数列{an}和数列{bn}中取项:
第1次从数列{an}中取a1,
第2次从数列{bn}中取b1,b2,
第3次从数列{an}中取a2,a3,a4,
第4次从数列{bn}中取b3,b4,b5,b6,
……
第2n-1次从数列{an}中继续依次取2n-1个项,
第2n次从数列{bn}中继续依次取2n个项,
… …
…
由此构造数列{cn}:a1,b1,b2,a2,a3,a4,b3,b4,b5,b6,a5,a6,a7,a8,a9,b7,b8,b9,b 10,b11,b12,…,记数列{cn}的前n和为Sn.求满足Sn<22014的最大正整数n.
10,b11,b12,…,记数列{cn}的前n和为Sn.求满足Sn<22014的最大正整数n.
查看答案和解析>>
科目:高中数学 来源: 题型:
某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出
前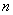 名学生,并对这
名学生,并对这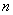 名学生按成绩分组,第一组
名学生按成绩分组,第一组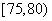 ,第二组
,第二组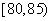 ,第三
,第三
组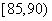 ,第四组
,第四组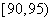 ,第五组
,第五组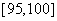 ,如图为频率分布直方图的一部分,
,如图为频率分布直方图的一部分,
其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组
的人数为60.
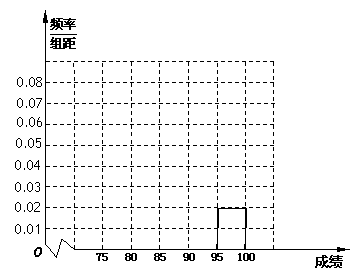
(I)请在图中补全频率分布直方图;
(II)若 大学决定在成绩高的第
大学决定在成绩高的第 ,
,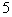 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取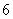 名学生,并且分成
名学生,并且分成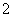 组,每组
组,每组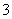 人进行面试,求
人进行面试,求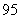 分(包括95分)以上的同学在同一个小组的概率.
分(包括95分)以上的同学在同一个小组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com