
某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出
前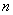 名学生,并对这
名学生,并对这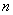 名学生按成绩分组,第一组
名学生按成绩分组,第一组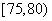 ,第二组
,第二组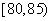 ,第三
,第三
组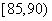 ,第四组
,第四组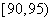 ,第五组
,第五组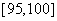 ,如图为频率分布直方图的一部分,
,如图为频率分布直方图的一部分,
其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组
的人数为60.
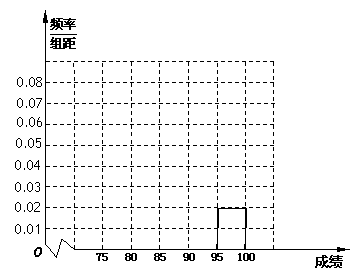
(I)请在图中补全频率分布直方图;
(II)若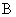 大学决定在成绩高的第
大学决定在成绩高的第 ,
,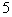 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取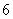 名学生,并且分成
名学生,并且分成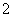 组,每组
组,每组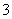 人进行面试,求
人进行面试,求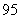 分(包括95分)以上的同学在同一个小组的概率.
分(包括95分)以上的同学在同一个小组的概率.
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:
已知在直角坐标系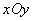 中,直线
中,直线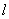
 的参数方程为
的参数方程为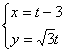 ,(
,(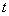 为参数),以坐标原点
为参数),以坐标原点
为极点,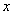 轴的正半轴为极轴建立极坐标系,曲
轴的正半轴为极轴建立极坐标系,曲 线
线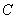 的极坐标方程为
的极坐标方程为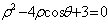
(I)求直线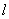 的普通方程和曲线
的普通方程和曲线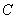 的直角坐标方程;
的直角坐标方程;
(II)设点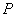 是曲线
是曲线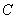 上的一个动点,求它到直线
上的一个动点,求它到直线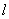 的距离
的距离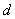 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线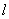 的参数方程为
的参数方程为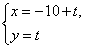 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为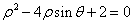 .
.
(Ⅰ)把圆C的极坐标方程化为直角坐标方程;
(Ⅱ)将直线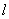 向右平移h个单位,所对直线
向右平移h个单位,所对直线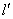 与圆C相切,求h.
与圆C相切,求h.
查看答案和解析>>
科目:高中数学 来源: 题型:
根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示
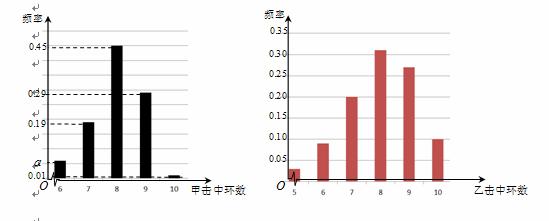
(Ⅰ)求上图中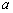 的值;
的值;
(Ⅱ)甲队员进行一次射击,求命中环数大于7环的概率(频率当作概率使用);
(Ⅲ)由上图判断甲、乙两名队员中,哪一名队员的射击成绩更稳定(结论不需证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com