
已知等差数列{an}、等比数列{bn}满足a1+a2=a3,b1b2=b3,且a3,a2+ b1,a1+ b2成等差数列,a1,a2,b2成等比数列.
(1)求数列{an}和数列{bn}的通项公式;
(2)按如下方法从数列{an}和数列{bn}中取项:
第1次从数列{an}中取a1,
第2次从数列{bn}中取b1,b2,
第3次从数列{an}中取a2,a3,a4,
第4次从数列{bn}中取b3,b4,b5,b6,
……
第2n-1次从数列{an}中继续依次取2n-1个项,
第2n次从数列{bn}中继续依次取2n个项,
… …
…
由此构造数列{cn}:a1,b1,b2,a2,a3,a4,b3,b4,b5,b6,a5,a6,a7,a8,a9,b7,b8,b9,b 10,b11,b12,…,记数列{cn}的前n和为Sn.求满足Sn<22014的最大正整数n.
10,b11,b12,…,记数列{cn}的前n和为Sn.求满足Sn<22014的最大正整数n.
(1)解:设等差数列{an}的公差为 ,等比数列{bn}的公比为
,等比数列{bn}的公比为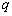 ,
,
依题意,得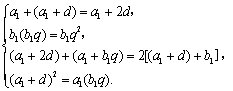 解得a1=d=1,b1=q=2.
解得a1=d=1,b1=q=2.
故an=n,bn=2n.…
(2)解:将a1,b1,b2记为第1组,a2,a3,a4,b3,b4,b5,b6记为第2组,a5,a6,a7,a8,a9,b7,b8,b9,b10,b11,b12记为第3组,……以此类推,则第n组中,有2n-1项选取于数列{an},有2 n项选取于数列{bn},前n组共有n2项选取于数列{an},有n2+n项选取于数列{bn},记它们的总和为Pn,并且有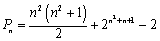 .
.
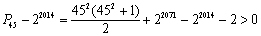 ,
,
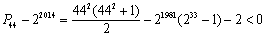 .
.
当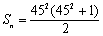 +(2+22+…+22012)时,
+(2+22+…+22012)时,
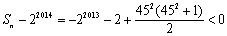 .当
.当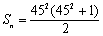 +(2+22+…+22013)时,
+(2+22+…+22013)时,
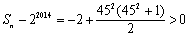 .
.
可得到符合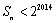 的最大的n=452+2012=4037.
的最大的n=452+2012=4037.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
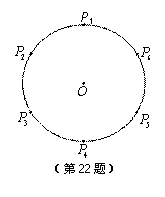
如图,设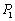 ,
,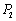 ,…,
,…,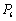 为单位圆上逆时针均匀分布的六个点.现任选其中三个不同点构成一
为单位圆上逆时针均匀分布的六个点.现任选其中三个不同点构成一
个三角形,记该三角形的面积为随机变量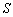 .
.
(1)求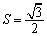 的概率;
的概率;
(2)求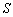 的分布列及数学期望
的分布列及数学期望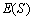 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知在直角坐标系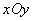 中,直线
中,直线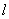
 的参数方程为
的参数方程为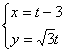 ,(
,(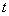 为参数),以坐标原点
为参数),以坐标原点
为极点,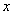 轴的正半轴为极轴建立极坐标系,曲
轴的正半轴为极轴建立极坐标系,曲 线
线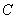 的极坐标方程为
的极坐标方程为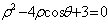
(I)求直线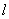 的普通方程和曲线
的普通方程和曲线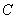 的直角坐标方程;
的直角坐标方程;
(II)设点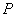 是曲线
是曲线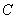 上的一个动点,求它到直线
上的一个动点,求它到直线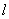 的距离
的距离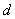 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com